Tangent length
There is a triangle ABC whose perimeter is 2s (2s = a + b + c), and the circle k (S, ρ) is the inscribed circle of the triangle. Calculate the length of the tangent of the circle k from point A.
Final Answer:
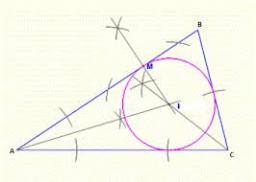
You need to know the following knowledge to solve this word math problem:
planimetricsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Triangle
 In triangle ABC, there is a point S with the center of the inscribed circle. The area of quadrilateral ABCS is equal to four-fifths of the area of triangle ABC. The lengths of the sides of triangle ABC expressed in centimeters are all integers and the
In triangle ABC, there is a point S with the center of the inscribed circle. The area of quadrilateral ABCS is equal to four-fifths of the area of triangle ABC. The lengths of the sides of triangle ABC expressed in centimeters are all integers and the - Intersection + tangents
 Given a circle with a radius r = 4 cm and a point A for which |AS| applies = 10 cm. Calculate the distance of point A from the intersection of the points of contact of the tangents drawn from point A to the circle.
Given a circle with a radius r = 4 cm and a point A for which |AS| applies = 10 cm. Calculate the distance of point A from the intersection of the points of contact of the tangents drawn from point A to the circle. - Circle inscribed
 There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26? - Triangle perimeter function
 Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis.
Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis. - Touch circle
 Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Given is
 Given is the circle x²+y²-4x+2y-11=0. Calculate the area of the regular hexagon inscribed in the given circle.
Given is the circle x²+y²-4x+2y-11=0. Calculate the area of the regular hexagon inscribed in the given circle. - Quarter circle
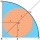 What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
