Intersection 74914
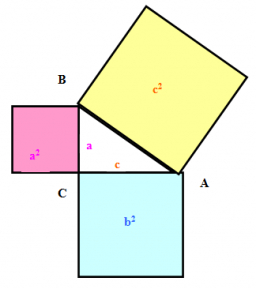
Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- analytic geometry
- algebra
- equation
- arithmetic
- square root
- absolute value
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Intersection 49623
Where is the intersection of the function y = -3x + 5 with the coordinate axes x and y? (where they are on the x-axis and y-axis) - Intersection of functions
Draw a graph of the function given by the equation y = -2x +3, find its intersections with the coordinate axes, and complete the unknown coordinates A [3;? ], B [?; 8]. - X-coordinate 81737
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - A Cartesian framework
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
- Intersections 62784
A quadratic function is given: y = -x² + 2x + 3 a) determine the intersections with the x, y-axis and peak V b) draw a graph and describe c) for which x applies f (x) = 3 - Coordinate
Determine the unknown coordinate of the point M [x, 54] of the graph of the function f by rule: y = 3x - Intersections
Find the intersections of the function plot with coordinate axes: f (x): y = x + 3/5
