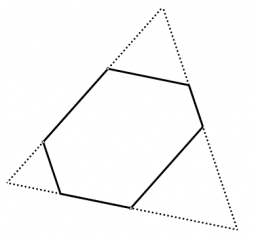
Irregular hexagon
There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and 193. What is its area?
Correct answer:
Showing 1 comment:
Math student
There is an irregular hexagon whose sides are the same length.
If a1=a2=a3=a4=a5=a6 it is regular hexagon.
There is an irregular hexagon whose opposite sides are the same length....
Then is a=87,18... b=135,68... c=137,99... d=360,84...
Area of hexagons is:
S=Sd-Sa-Sb-Sc =36875,1 (Sd; Sa; Sb; Sc is area of equilateral triangels).
If a1=a2=a3=a4=a5=a6 it is regular hexagon.
There is an irregular hexagon whose opposite sides are the same length....
Then is a=87,18... b=135,68... c=137,99... d=360,84...
Area of hexagons is:
S=Sd-Sa-Sb-Sc =36875,1 (Sd; Sa; Sb; Sc is area of equilateral triangels).
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsGrade of the word problem
Related math problems and questions:
- Garden
The garden has two opposite parallel fences. Their distance is 33.1 m. The lengths of these two fences are 75.5 meters and 49.4 meters. Calculate the area of this garden. - Trapezium
The lengths of parallel sides of a trapezium are (2x+3) and (x+8), and the distance between them is (x+4). If the area of the trapezium is 590, find the value of x. - Hexagon 5
The distance of parallel sides of regular hexagons is 61 cm. Calculate the length of the radius of the circle described in this hexagon. - Garden
Trapezoid garden has parallel sides 19 m and 24 m. Its area is 193.5 square meters. What is the width of the garden?
- Semicircles
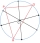In a rectangle with sides of 4cm and 8cm, there are two different semicircles, each of which has its endpoints at its adjacent vertices and touches the opposite side. Construct a square such that its two vertices lie on one semicircle, the remaining two o - Inscribed 43991
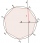An irregular convex octagon is inscribed in the circle. Its four adjacent sides have a length of 3, and the remaining four adjacent sides have a size of 2. What is the area of a given octagon? - Irregular
Calculate the area and perimeter of the garden that was created from a rectangular plot measuring 10 by 20 meters after transferring one corner measuring 6 by 7 meters. The separated rectangular plot has parallel sides to the main plot. Did the perimeter
