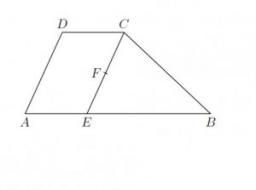
Trapezium
The lengths of parallel sides of a trapezium are (2x+3) and (x+8), and the distance between them is (x+4). If the area of the trapezium is 590, find the value of x.
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Perpendicular and parallel
 Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines?
Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines? - Parallel lines - dist
 Find the distance between the parallel lines 3x – 4y +7 = 0 and 3x – 4y + 5 = 0
Find the distance between the parallel lines 3x – 4y +7 = 0 and 3x – 4y + 5 = 0 - A field
 A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m and the non parallel sides are 14 m and 13 m. Find the area of the field.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m and the non parallel sides are 14 m and 13 m. Find the area of the field. - Sunflower Field
 The trapezoidal sunflower field is located between two parallel paths spaced 230 meters apart. The lengths of the parallel sides of the field are 255 m and 274 m. How many tons of sunflower will come from this field if the hectare yield is 2.25 tons?
The trapezoidal sunflower field is located between two parallel paths spaced 230 meters apart. The lengths of the parallel sides of the field are 255 m and 274 m. How many tons of sunflower will come from this field if the hectare yield is 2.25 tons? - Irregular hexagon
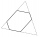 There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and 193. What is its area?
There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and 193. What is its area? - Distance two imaginary numbs
 Find the distance between two complex numbers: z1=(-8+i) and z2=(-1+i).
Find the distance between two complex numbers: z1=(-8+i) and z2=(-1+i). - Two chords
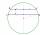 In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle.
In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle.
