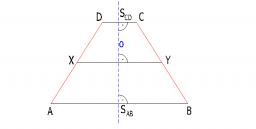
Trapezium internal angles
A trapezium where AB is parallel to CD, has angle A : angle D = 4 :5, angle B = 3x-15 and angle C = 4x+20. Find angle A, B, C and D.
Correct answer:
Showing 1 comment:
Partho
Let Angle A=4x, B= 3x-15, C=4x+20 and D=5x.
Using the property that sum of adjacent angles = 180 we get:
A + D = 180 or 4x+5x=180.
Solving we get x=20.
Substituting we get: A=80, B=100
Similarly, B+C=180 or
3x-15+4x+20=180
Solving we get x=25
Substituting we get: B=60, D=120.
Using the property that sum of adjacent angles = 180 we get:
A + D = 180 or 4x+5x=180.
Solving we get x=20.
Substituting we get: A=80, B=100
Similarly, B+C=180 or
3x-15+4x+20=180
Solving we get x=25
Substituting we get: B=60, D=120.
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Trapezium ABCD
The figure shows ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ=JK=KP. If AB=0.5m and AP=BQ=1.8m, find the lengths of AC, BD, RN, and LM. angle D=angle C=60 - Four-digit 55481
Find all four-digit abcd numbers to which abcd = 20. ab + 16. cd, where ab and cd are double digits numbers from digits a, b, c, and d. - Swimming pool
A swimming pool 30 meters long is filled with water to a depth of 1 meter at the shallow end, and 5 meters at the deep end, and abcd the vertical area of the pool has the shape of a trapezium with the area given by S(abcd)= 1/2 (ab + cd) x ad. What is the - Trapezoid RT
The plot is a rectangular trapezium ABCD, where ABIICD has a right angle at the vertex B side and AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. The lengths of the sides AB and CD are in the ratio 3:2. Calculate the con
- Parallel and orthogonal
I need math help in this problem: a=(-5, 5 3) b=(-2,-4,-5) (they are vectors) Decompose the vector b into b=v+w where v is parallel to a and w is orthogonal to a, find v and w - Trapezium
The lengths of parallel sides of a trapezium are (2x+3) and (x+8), and the distance between them is (x+4). If the area of the trapezium is 590, find the value of x. - One trapezium
One trapezium has AB=24M, BC=36M, CD=80M, DA=80M long sides. Find the area.
