Rhombus MATH
Construct a rhombus M A T H with diagonal MT=4cm, angle MAT=120°
Final Answer:

Showing 1 comment:
Solustion2
Constructions steps:
1. make angle XAY = 120 deg
2. draw its axis p througth point A....
3. draw two paralels lines l1,l2 to axis p at distance 4/2 = 2 cm
4. intersections of legs of angle XAY and l1, l2 is points is points M and T.
5. make point H - use symmetry of point A in mirror of line MTrhombus
1. make angle XAY = 120 deg
2. draw its axis p througth point A....
3. draw two paralels lines l1,l2 to axis p at distance 4/2 = 2 cm
4. intersections of legs of angle XAY and l1, l2 is points is points M and T.
5. make point H - use symmetry of point A in mirror of line MTrhombus
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesthemes, topicsGrade of the word problem
Related math problems and questions:
- Rhombus construct
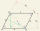 Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm.
Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm. - Construct 61354
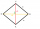 Construct an ABCD diamond with side a = 4.8cm, and the angle at vertex B is 60 °
Construct an ABCD diamond with side a = 4.8cm, and the angle at vertex B is 60 ° - Quadrilateral 27693
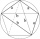 Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125°
Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125° - Diagonals
 Construct a rhombus whose diagonals have lengths of 10cm and 8cm and make an angle of 115°.
Construct a rhombus whose diagonals have lengths of 10cm and 8cm and make an angle of 115°. - Square equal rhombus
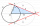 Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm, and angle |DAB| = 30°.
Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm, and angle |DAB| = 30°. - Construct 22
 Construct a rhombus ABCD if the diagonals are f=7cm, e=5 cm.
Construct a rhombus ABCD if the diagonals are f=7cm, e=5 cm. - Construct 5593
 Construct an isosceles trapezoid, whose base is 6 cm long, the base forms an angle of 30 ° with the diagonal, and the arms are 4 cm long.
Construct an isosceles trapezoid, whose base is 6 cm long, the base forms an angle of 30 ° with the diagonal, and the arms are 4 cm long.
