Cross section
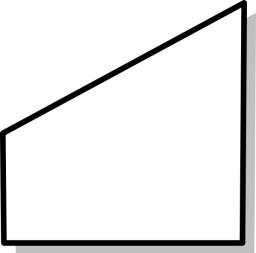
The cross-section ABCD of a swimming pool is a trapezium. Its width AB=14 meters, depth at the shallow end is 1.5 meters, and at the deep end is 8 meters. Find the area of the cross-section.
Correct answer:
Showing 6 comments:
George
a fiberglass pool that is 12.3 wide and 23.9 long and is 3'9-5'11 deep, would need how many panels?
5 years ago 1 Like
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Swimming pool
A swimming pool 30 meters long is filled with water to a depth of 1 meter at the shallow end, and 5 meters at the deep end, and abcd the vertical area of the pool has the shape of a trapezium with the area given by S(abcd)= 1/2 (ab + cd) x ad. What is the - Cross-section 32163
The bottom of the garden pool of circular cross-section has an inner diameter of d = 4 m. The water depth is 0.8 m. How many liters of water can we fill into the pool? - Area of ditch
How great will an area have a section of the trapezoidal ditch with a width of 1.6 meters above and below 0.57 meters? The depth of the ditch is 2.08 meters. - Swimming pool 7
The perimeter of a rectangular swimming pool is 20 4/5 meters. Its length is thrice its width. What is the length of the pool? What is its width? - Cross-sectional 18973
Calculate the cross-sectional area of the trapezoidal channel irrigation channel if its upper width is 7.9 m, its bottom width is 5.5 m, and its depth is 2.8 m. - Trapezium ABCD
The figure shows ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ=JK=KP. If AB=0.5m and AP=BQ=1.8m, find the lengths of AC, BD, RN, and LM. angle D=angle C=60 - Three-quarters 6192
The swimming pool in the Veselý yard is square-shaped with dimensions of 2.5m by 3.4m and is 1.7 meters deep. How many liters are in the pool if it is filled to three-quarters of its total volume? Please round the result to tenths. - Slope of the pool
Calculate the slope (rise:run) of the bottom of the swimming pool long 10 m. The water depth at the beginning of the pool is 0.96 m (for children), and the depth at the end is 1.86 m (for swimmers). Slope express as a percentage and as the angle in degree - Cross-section 79984
A ditch with a cross-section in the shape of an isosceles trapezoid with bases of 3 m and 5 m and arms of length 2 m is 2.5 meters deep and 10 meters long. How many cubic meters of soil did they have to excavate when digging it? - Trapezoid - intersection of diagonals
In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area. - Cross-section 46841
The cross-section of the channel has the shape of a trapezoid. The bottom width is 2.25 m, and the depth is 5 m. The walls have a slope of 68°12' and 73°45'. Calculate the upper channel width. - Pool
The swimming pool is 10 m wide and 8 m long, and 153 cm deep. How many hectoliters of water are in it if the water is 30 cm below its upper edge? - Three-quarters of its volume
The pool has a block shape with a length of 8m, a width of 5.3m, and a depth of 1.5m. How many hectoliters of water is in it if it is filled to three-quarters of its volume? - Drainage channel
The cross-section of the drainage channel is an isosceles trapezoid whose bases have a length of 1.80 m and 0.90 m, and the arm has a length of 0.60 meters. Calculate the depth of the channel. - Length 6235
Length 25m, width 10m, depth 160 cm. How many square meters are needed to line the pool? - Children's pool
The children's pool at swimming pool is 10m long, 5m wide, and 50cm deep. Calculate: (a) how many m² of tiles are needed for lining the perimeter walls of the pool? (b) how many hectoliters of water will fit into the pool? - Trapezium diagonals
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC.
