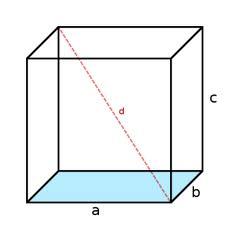
Cube - angles
Calculate the angle alpha (α) between the wall diagonal and cube base. Calculate the angle beta (β) between the cube body diagonal and the cube base.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- arithmetic
- square root
- solid geometry
- cube
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- goniometry and trigonometry
- tangent
- arctangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Box
Calculate the angle between box base 9 x 14 and body diagonal length 18. - Task
I have homework. The cube's edge is 7 cm long, and I must find the diagonal between the wall and the body. - Quadrilateral pyramid
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Remaining 25441
An isosceles triangle has the size of the angles at the base alpha = beta = 34 degrees 34 minutes. Calculate the magnitude of the angle at the remaining vertex of the triangle in degrees and minutes.
- Calculate 64654
Calculate the length of the wall and body diagonal in a cube with an edge of 60 cm. - Diagonals 7084
Calculate the lengths of the wall and body diagonals of the cube with an edge length of 10 cm. - Angles in triangle
Calculate the angle alpha in the triangle if the beta is 61 degrees and 98 gamma degrees.
