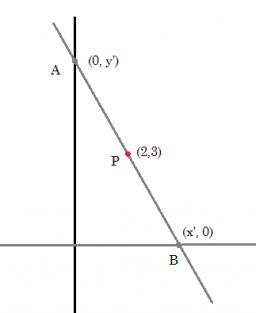
Coordinate axes
Find the triangle area given by line -7x+7y+63=0 and coordinate axes x and y.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- XY triangle
Determine the area of a triangle given by line 2x-4y+47=0 and coordinate axes x and y. - Intersection of functions
Draw a graph of the function given by the equation y = -2x +3, find its intersections with the coordinate axes, and complete the unknown coordinates A [3;? ], B [?; 8]. - Intersections
Find the intersections of the function plot with coordinate axes: f (x): y = x + 3/5 - Line intersect segment
Decide whether the line p : x + 2 y - 7 = 0 intersects the line segment given by points A[1, 1] and B[5, 3]
- Coordinate 82855
What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system? - Ellipse
Ellipse is expressed by equation 9x² + 25y² - 54x - 100y - 44 = 0. Find the length of primary and secondary axes, eccentricity, and coordinates of the ellipse's center. - Intersection 49623
Where is the intersection of the function y = -3x + 5 with the coordinate axes x and y? (where they are on the x-axis and y-axis)
