Midpoint of segment
Find the distance and midpoint between A(1,2) and B(5,5).
Correct answer:
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
See also our right triangle calculator.
Looking for a statistical calculator?
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Points on line segment
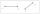Points P and Q belong to segment AB. If AB=a, AP = 2PQ = 2QB, find the distance between point A and the midpoint of segment QB. - Midpoint 11
Consider the following line segment - start point A=(-4,1), endpoint B=(4,-1). Find the midpoint. Please show your work. - Midpoint between conjugate
Find the midpoint between two roots: 2+3.464i and 2 - 3.464i - Midpoint 6
For line segment length is given: FM=8a+1, FG=42. Point M is the midpoint of FG. Find unknown a.
- Midpoint 5 FM=3x-4, MG=5x-26, FG=? Point M is the midpoint of FG. Use the given information to find the missing measure or value.
- Construct 8
Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati - Equation of the circle
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0
