Ditch
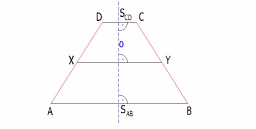
The ditch profile is an isosceles trapezoid with bases of length 80m and 60m. The slope of the sidewall of the ditch is 80°. Calculate the ditch depth.
Correct answer:
Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Calculation of an isosceles triangle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The ditch
Ditch with a cross-section of an isosceles trapezoid with bases 2m and 6m deep 1.5m. How long is the slope of the ditch? - Cross-section - digging
How many m³ of soil is to be excavated when digging a 120 m long ditch, the cross-section of which is an isosceles trapezoid with bases of 2.3 m and 3.3 m, if the depth of the trench is 90 cm? - Drainage channel
The drainage channel's cross-section is an isosceles trapezoid whose bases are 1.80 m and 0.90 m long, and the arm is 0.60 meters long. Calculate the channel's depth. - Isosceles ditch
A ditch with a cross-section in the shape of an isosceles trapezoid with bases of 3 m and 5 m and arms of length 2 m is 2.5 meters deep and 10 meters long. How many cubic meters of soil did they have to excavate when digging it? - The isosceles
The isosceles trapezoid ABCD has bases of 18 cm and 12 cm. The angle at apex A is 60°. What is the circumference and area of the trapezoid? - An isosceles trapezoid
An isosceles trapezoid has base angles of 50° each, and its bases are 20 cm and 30 cm. Compute its area. - Cross-section - trapezoid
The cross-section of the channel has the shape of a trapezoid. The bottom width is 2.25 m, and the depth is 5 m. The walls have a slope of 68°12' and 73°45'. Calculate the upper channel width.
