Lampshade
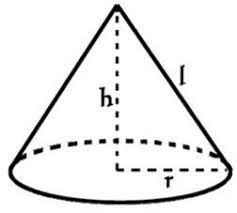
The cone-shaped lampshade has a diameter of 30 cm and a height of 10 cm. How many cm2 of material will we need when 10% is waste?
Final Answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Lampshade 3
The lampshade has the shape of a rotating cone shell with a side of 32 cm and a base diameter of 46 cm. Calculate the paper consumption for its production if you assume that the waste will be 6% - Twenty percent
The students in the class agreed to make various decorative cone-shaped hats for the carnival. How much decorative material did a class of 25 students need to make the hats, if they had to count on about twenty percent waste when cutting and gluing? (The - Lamp cone
Calculate the surface of a lampshade shaped like a rotary truncated cone with a base diameter of 32 cm and 12 cm and a height of 24 cm. - How many
How many m² of copper sheet is needed to replace the roof of a conical tower with a diameter of 13 meters and a height of 24 meters if we count 8% of the material for bending and waste? - Calculate 82409
The lamp shade should be formed by the shell of a cone with a base diameter of 48 cm and a side of 32 cm. Calculate how much material will be needed to make it, assuming 8% waste - Iglu - cone tent
The cone-shaped tent is 3 m high, and the diameter of its base is 3.2 m. a) The tent is made of two layers of material. How many m² of fabric is needed for production (including flooring) if 20% needs to be added to the minimum amount due to cutting waste - Church roof 2
The roof has the shape of a rotating cone shell with a base diameter of 6 m and a height of 2.5 m. How much money (CZK) will cost the roof cover sheet if 1 m² of metal sheet costs 152 CZK and if you need 15% extra for joints, overlays, and waste?
