Reciprocal equation 2
Solve this equation:
x + 5/x - 6 = 4/11
x + 5/x - 6 = 4/11
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebrabasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Solve 18
Solve simple equation: 3x = 5x + 6/2x + 3 - Fraction + eq
Solve following simple equation with fractions: -5/6(8+5b) = 75 + 5/3b - Simply equation
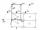Solve this equation for x: 9x-6(x-1)=5(x+2)-14 - Equation
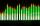Solve the equation and check the result: 1.6x - 3/2 + x - 9,8 = x + 0,4/3 - 7 + 1,6/6 - Equation 25
Solve the following simple equation: 3/4(x+5)=1/2(x+9) - Adding mixed 3
Why does 1 3/4 + 2 9/10 equal 4.65? How do you solve this? - Equation: 4006
Solve the equation: (4x / 2.5x) + (2.4: x) = 3.1. x is a natural number.
