Cube root
Find the cube root of 18
Correct answer:
You need to know the following knowledge to solve this word math problem:
algebraarithmeticnumbersGrade of the word problem
Related math problems and questions:
- Cbrt of fraction
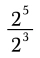If a fraction is multiplied by itself and then divided by the reciprocal of the same fraction, the result is 18 26/27. Find the fraction. - Geometric 20
Find the geometric mean of 15 15 20 25 30. - Complex roots
Find the sum of the fourth square root of the number 16. - Geometric progression
If the 6th term of a GP is four and the 10th is 4/81, find common ratio r.
- Binary series
The 4th term of a G.P. is 16 and the 7th term is 128 . Find the first term and common ratio of the series. - The volume 2
The volume of a cube is 27 cubic meters. Find the height of the cube. - Three members GP
The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers.
