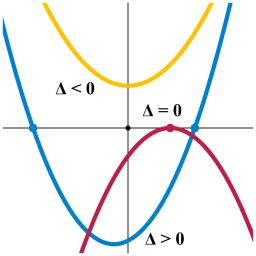
Discriminant

Determine the discriminant of the equation:

3 x^{2} + 19 = 4

Final Answer:

Did you find an error or inaccuracy? Feel free to send us. Thank you!

Tips for related online calculators

Are you looking for help with calculating roots of a quadratic equation?

You need to know the following knowledge to solve this word math problem:

algebra

quadratic equation

Grade of the word problem

high school

Related math problems and questions:

Has infinity many solutions
Solve the equation and determine the type of solution the equation has. Select all possible answers. 6y+9=3(2y+3)
Roots and coefficient
In the equation 2x² + bx-9 = 0 is one root x1 = -3/2. Determine the second root and the coefficient b.
Coefficient 21623
In the equation 2x² + bx-9 = 0 there is one root x1 = -3 / 2. Determine the second root and the coefficient b
Expression 68414
The expression 3x - [2 - (2x - 1) + x] is given. Determine for which number x the expression is equal to 0.
Equation
Equation -3x²+bx -108 =0 has one root x₁ = 1. Determine the coefficient b and the second root x₂.
Zero fraction equation
Find the value of y: 3/5y-9/4 (y +4) -1 = 1/2 (3y-2) -3 (3-y)
Equation 25
Solve the following simple equation: 3/4(x+5)=1/2(x+9)