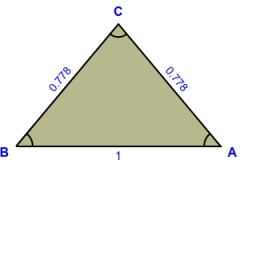
Angle at the apex
In an isosceles triangle, the angle at the apex is 30° greater than the angle at the base. How big are the internal angles?
Correct answer:
Tips for related online calculators
Do you have a system of equations and are looking for calculator system of linear equations?
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Inner angles
The magnitude of the internal angle at the central vertex C of the isosceles triangle ABC is 72°. The line p, parallel to the base of this triangle, divides the triangle into a trapezoid and a smaller triangle. How big are the inner angles of the trapezoi - Determine 82143
Determine the size of the interior angles in an isosceles triangle if you know that the angle opposite the base is 15° greater than the angles at the base. - Magnitude 23271
In an isosceles triangle, the angle at the primary vertex is 20 ° smaller than twice the magnitude of the angle at the base. What are the interior angles of a triangle? - Calculate 71764
The angle at the base of an isosceles triangle is 18 ° larger than the angle at the central vertex. Calculate the size of the interior angles.
- Isosceles 81130 The angle at the apex of an isosceles triangle is 78°. Base 28.5cm. Shoulder length?
- Triangle angles
In a triangle, ABC, the interior angle at vertex C is twice the internal angle at point A. The outer angle at point B measured 117 degrees. How big is the external angle at vertex A? - An isosceles
An isosceles trapezoid has base angles of 50° each, and its bases are 20 cm and 30 cm. Compute its area.
