Garrett
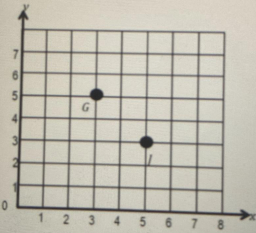
Garrett and Jeffrey are planning a treasure hunt. They decide to place a treasure at a point that is a distance of 5 units from the x-axis and three units from the y-axis. Jeffrey places a treasure at point J at coordinates (5,3), and Garrett places one at point G=(3,5). Who put the treasure in the right place? Explain how you know.
Correct answer:
You need to know the following knowledge to solve this word math problem:
geometryGrade of the word problem
Related math problems and questions:
- X-coordinate 81737
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - A Cartesian framework
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Sarah 4
Sarah and Jamal were learning partners in math class and were working independently. They each started at the point (−2, 5) and moved 3 units vertically in the plane. Each student arrived at a different endpoint. How is this possible? Explain and list the - Vertical axis Find the perpendicular distance of the point A=(5,-7) from the y-axis.
- School group
There are five girls and seven boys in the group. They sit in a row next to each other. How many options if no two girls sit next to each other? - You leave
You leave school at the end of the day and walk 3/8 of a mile away before realizing that you left your backpack and immediately turn around. You then walk 1/6 of a mile back towards school at this point. Assuming you walked in a straight line, how many mi - Determine 8133
Determine the distance between two places, M, and N, between which there is an obstacle so that place N is not visible from place M. The angles MAN = 130°, NBM = 109°, and the distances |AM| = 54, |BM| = 60, while the points A, B, and M lie on one straigh
