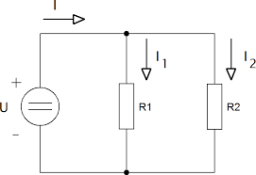
Resistance 80351

We connected two resistors in parallel in the circuit, with the first having three times the resistance of the second. The voltage between the terminals of each resistor is 6 V. Calculate the current through each branch when the resulting resistance of both resistors is 15 ohms.

Final Answer:

I₁ =  0.1 A
I₂ =  0.3 A

Step-by-step explanation:

$$\begin{gathered} U=6\text{V} \\ R=15\Omega \\ {R}_1=3\cdot R_2 \\ 1/R=1/R_1+1/R_2 \\ I=U/R=6/15=\frac{2}{5}=0.4\text{A} \\ I=I_1+I_2 \\ {I}_1:I_2=R_2:R_1=R_2:3R_2=1:3 \\ {I}_1=I\cdot \frac{1}{1+3}=0.4\cdot \frac{1}{1+3}=0.1\text{A} \end{gathered}$$

$I_2=I-I_1=0.4-0.1=0.3\text{A}$

Try another example