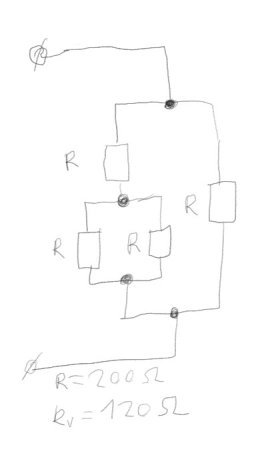
Several resistors

We have a box with the same resistors, so all of them have a resistance value of 200 ohms. Draw the connection of several resistors so that the resulting resistance is: a) 100 b) 120 (only 4 resistors)

Final Answer:

R₁ =  100 Ω
R₂ =  120 Ω

Step-by-step explanation:

$$\begin{gathered} R=200\Omega \\ 100\Omega =R||R \\ {R}_1=\frac{R\cdot R}{R+R}=\frac{200\cdot 200}{200+200}=100\Omega \end{gathered}$$

$$\begin{gathered} R_8=120\Omega \\ {R}_8=\frac{x\cdot R}{x+R} \\ {R}_8\cdot x+R_8\cdot R=x\cdot R \\ x=\frac{R_8\cdot R}{R-R_8}=\frac{120\cdot 200}{200-120}=300\Omega \\ x=R+R_1\Omega \\ {R}_2=\frac{x\cdot R}{x+R}=\frac{300\cdot 200}{300+200}\Omega =120\Omega \end{gathered}$$

Try another example