A jackpot
How many times must I play this jackpot to win?
A jackpot of seven games having (1 X 2), i.e., home win or away win.
A jackpot of seven games having (1 X 2), i.e., home win or away win.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
combinatoricsbasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Pet store 2
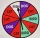A pet store is having a prize giveaway. The spinner shows the type of toy a customer can win for their pet. If a customer spins the spinner and it lands on a cat, they will win a free cat toy. If the spinner is spun 540 times throughout the day, about how - Play video game
Tyson plays video games about 2 1/2 times more than the average kid. His mother thinks that he should cut down on his playing time by 1/4 of the time. How will Tyson's gaming compare to the average kid's if he makes this change? - Game 27
Susan wanted to play the game. In the beginning, the first says a number from 1 to 8. Then the second player adds a number from 1 to 5 and tells the sum. Again, Susan adds a number from 1-5 and says sum, etc. The winner must say the number 27. What first - Beginning 2711
Jano likes to play various games for beans. He recently played two games with Peter. In the first game, he won 32 beans; in the second game, he lost 75 beans. How was Jano after these two parties? Did he have more or less beans than at the beginning? And - Guaranteed 37611
Determine how many different ways a Lotto ticket can be written if we guess six numbers out of 49. At what Jackpot would it already pay to bet so many tickets to be guaranteed to win the 1st prize? The price of one type is €1. - Playing games
In a school, 9/10 of the students take part. 2/3 of these play football. What fraction of the students play football? - Sometimes 2814
Adam was at some of his favorite football team's home games last season. Sometimes, he bought a seat ticket for €9, sometimes a standing ticket for €5. He spent a total of €76. How many times did Adam buy a seat ticket, and how many times did he buy a sta
