Positive products
Which of these products is positive?
Select all that apply.
a) -0.2 * (12.5)
b) -4.7 * (-1)
Result
Select all that apply.
a) -0.2 * (12.5)
b) -4.7 * (-1)
Result
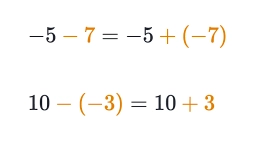
You need to know the following knowledge to solve this word math problem:
arithmeticnumbersGrade of the word problem
Related math problems and questions:
- In which
In which of the following expressions does the number 16 fill in the blank so that the equation is true? Select all that apply. A) 8(___ + 3) = 32 + 24 B) 8(2 + 9) = ___ + 72 C) 4(7 + 4) = 28 + ___ D) 8(5 + 6) = 40 + ___ - Once simplified
Once simplified, which of the expressions below has a value between 20 and 30? Select all that apply. A) 32÷8×514 B) -18÷6×9 C) 4×12÷2 D) 12×413÷(-2) - Horseback riding
The total cost to go horseback riding is x dollars per hour plus a $2 fee for renting a helmet. Which expressions represent the cost, in dollars, for 4 people to go horseback riding for 3 hours each? Select all that apply. Responses: A = 4(3x+2) B = 3(4x+ - In the shipment
There are 40 products in the shipment. Of these, 4 are defective. In how many ways can we select 5 products so that exactly 3 of them are good?
- Student examination
How many ways can a teacher select a group of 6 students to sit in the front row if the class has 13 students? - Parallel lines - dist
Find the distance between the parallel lines 3x – 4y +7 = 0 and 3x – 4y + 5 = 0 - Two geometric progressions
Insert several numbers between numbers 6 and 384 so that they form with the given GP numbers and that the following applies: a) the sum of all numbers is 510 And for another GP to apply: b) the sum of entered numbers is -132 (These are two different geome
