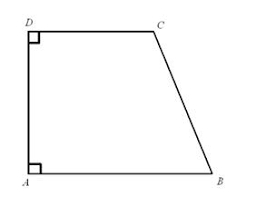
Rectangular trapezoid

In a rectangular trapezoid ABCD with right angles at vertices A and D with sides a = 12cm, b = 13cm, c = 7cm. Find the angles beta and gamma and height v.

Correct answer:

v =  12 cm
B =  67.3801 °
C =  112.6199 °

Step-by-step explanation:

$$\begin{gathered} a=12\text{ cm } \\ b=13\text{ cm } \\ c=7\text{ cm } \\ x=a-c=12-7=5\text{ cm } \\ v=\sqrt{b^2-x^2}=\sqrt{13^2-5^2}\text{ cm}=12\text{ cm} \end{gathered}$$

$B={\displaystyle \frac{180^{\circ }}{\pi }}\cdot \arcsin (v\mathrm{/}b)={\displaystyle \frac{180^{\circ }}{\pi }}\cdot \arcsin (12\mathrm{/}13)=67.3801^{\circ }=67^{\circ }22^{\mathrm{\prime }}49\mathrm{"}$

$C=180-B=180-67.3801=112.6199^{\circ }=112^{\circ }37^{\mathrm{\prime }}11\mathrm{"}$

Try another example

Related math problems and questions:

• Rectangular trapezoid
  The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid.
• Diagonal BD
  Find the length of the diagonal BD in a rectangular trapezoid ABCD with a right angle at vertex A when/AD / = 8,1 cm and the angle DBA is 42°
• Right triangle
  It is given a right triangle angle alpha of 90 degrees beta angle of 55 degrees c = 10 cm use Pythagorean theorem to calculate sides a and b
• IS trapezoid
  Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm.
• Rectangular
  Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle
• The sides 2
  The sides of a trapezoid are in the ratio 2:5:8:5. The trapezoid’s area is 245. Find the height and the perimeter of the trapezoid.
• Rectangular trapezoid
  The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate trapezium area in cm square and calculate how many differs perimeters of the
• Isosceles trapezoid
  Find the area of an isosceles trapezoid, if the bases are 12 cm and 20 cm, the length of the arm is 16 cm
• Median
  In triangle ABC is given side a=10 cm and median ta= 13 cm and angle gamma 90°. Calculate length of the median tb.
• The bases
  The bases of the isosceles trapezoid ABCD have lengths of 10 cm and 6 cm. Its arms form an angle α = 50˚ with a longer base. Calculate the circumference and content of the ABCD trapezoid.
• Right triangle trigonometrics
  Calculate the size of the remaining sides and angles of a right triangle ABC if it is given: b = 10 cm; c = 20 cm; angle alpha = 60° and the angle beta = 30° (use the Pythagorean theorem and functions sine, cosine, tangent, cotangent)
• Isosceles trapezoid
  What is the height of an isosceles trapezoid, the base of which has a length of 11 cm and 8 cm and whose legs measure 2.5 cm?
• Ratio in trapezium
  The height v and the base a, c in the trapezoid ABCD are in the ratio 1: 6: 3, its content S = 324 square cm. Peak angle B = 35 degrees. Determine the perimeter of the trapezoid
• Diagonal
  The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal.
• Space diagonal angles
  Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28cm, b = 45cm and c = 73cm. Then, find the angle between the body diagonal and the plane of the base ABCD.
• A trapezoid
  A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48° and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid.
• Area of iso-trap
  Find the area of an isosceles trapezoid if the lengths of its bases are 16 cm and 30 cm, and the diagonals are perpendicular to each other.