Algebra - math word problems - page 112 of 303
Number of problems found: 6056
- Apprentice 83169
The master gave the apprentice the task of dividing the 28 m long electric cable into two parts so that the second part was 2.5 times larger than the first. How long were the cable sections supposed to be? - Textbooks
A math textbook is 1 4/7 inches thick. How many of these books will fit on a 22-inch self? - Difference 5867
Calculate the value of the first term and the difference in the arithmetic sequence a1 + a7 = 42 a10-a3 = 21 - Six people
Six people who get the same salary arrange them in increasing order of their savings and also mention who saves the most Anil 1/3. Duma 2/5. Niki 1/4.CAI 2/3. Kat 3/4. Boo 1/2. - The ages
The ages of the four sons make an arithmetic sequence, the sum of which is the father's age today. In three years, the father's age will be the sum of the ages of the three eldest sons, and in the next two and three months, the father's age will be the su - The four
The four pirates divided 65 coins into each other. They were sorted by age, the youngest receiving the least number of coins, each half more than the previous one. How many coins did the oldest pirate receive? - Arithmetic progression
In some arithmetic progression applies: 5a2 + 7a5 = 90 s3 = 12 Find the first member a =? and difference d =. - School books
At the beginning of the school year, the teacher distributed 480 workbooks and 220 textbooks. How many pupils could have the most in the classroom? - Gearing
Gearing consists of two wheels. One is 88, and the second is 56 teeth. How many times turn the smaller wheel to hit the same teeth as in the beginning? How many times will we turn the biggest wheel? - Trio
A trio of workers earns 770 euros. Money is divided by the work that each of them makes. The first received twice the second, and the second received three times more than the third. How many got everyone's workers? - Theater
Each row of the theater has 15 seats. The ticket to the first 7 rows is for 26 EUR. The next row is for 13 EUR. The theater was completely sold out. Revenue was 5850 EUR. How many rows are in the theater? - Different 44621
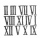Express the number 68 as this property's sum of two different summands. If you divide a larger sum by a smaller sum, will you receive a result of 3? - Finite arithmetic sequence
How many numbers should be inserted between the numbers 1 and 25 so that all numbers create a finite arithmetic sequence and that the sum of all members of this group is 117? - Shelves 7633
Juraj had music CDs and DVDs stored on the shelves. There are a total of 64. How many DVDs are on the shelf if there are seven times less than a CD? - Divisible without remainder
Determine the number by which all these numbers, 22, 18, 25, 15, 35, and 10, are divisible without remainder. The number is greater than 1. - Equivalent expression
Pablo rewrites the expression 8y-24 as 8(y-3). Hana rewrites 8y-24 as 2(4y-12). Are Pablo's and Hana's expressions each equivalent to 8y-24? Explain your reasoning. - Trolleybus 5729
How do pupils travel to school? 2/7 uses a trolley bus, 1/5 drives, and the remaining 136 pupils walk. How many pupils are there at school? - Which 13 Which numbers are perfectly divisible by 3? 45,904 40,404 145,083 16,674 75,035 (use sum of digits)
- Resulting 55991
The 180 cm long bar should be cut into two parts so that the longer part is 4 cm shorter than three times, the shorter part. Find the lengths of the resulting bar sections. - Cheese consumption
I have some cheese. I used 2/5 of the total amount of cheese yesterday. Today, I used 2/5 of the remaining cheese from yesterday. If 900 g of cheese remains at the end of today, how many grams of cheese did I have initially?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
