Angle practice problems - page 37 of 64
Number of problems found: 1262
- Triangle ABC v2
 The area of the triangle is 12 cm square. Angle ACB = 30º , AC = (x + 2) cm, BC = x cm. Calculate the value of x.
The area of the triangle is 12 cm square. Angle ACB = 30º , AC = (x + 2) cm, BC = x cm. Calculate the value of x. - Garage
 There are two laths in the garage opposite one another: one 2 meters long and the second 3 meters long. They fall against each other and stay against the opposite walls of the garage. Both laths cross 70 cm above the garage floor. How wide is the garage?
There are two laths in the garage opposite one another: one 2 meters long and the second 3 meters long. They fall against each other and stay against the opposite walls of the garage. Both laths cross 70 cm above the garage floor. How wide is the garage? - Determine 81756
 The area for shooting training has the shape of a trapezoid, the parallel sides of which are 36m, 21m long, and the remaining sides are 14m, 16m long. Determine the size of the interior angles with a longer base.
The area for shooting training has the shape of a trapezoid, the parallel sides of which are 36m, 21m long, and the remaining sides are 14m, 16m long. Determine the size of the interior angles with a longer base. - Shadow 7838
 A man 1.65 m tall casts a shadow of 1.25 m. How tall is the tree whose shadow is in debt 2.58 m?
A man 1.65 m tall casts a shadow of 1.25 m. How tall is the tree whose shadow is in debt 2.58 m? - Similarity n-gon
 6-gones ABCDEF and A'B'C'D'E'F' are similar. The area of 6-gon ABCDEF is S1=248 m², and the diagonal length FA is 28 m. Calculate the area of the 6-gon A'B'C'D'E'F' if F'A' = 36 m.
6-gones ABCDEF and A'B'C'D'E'F' are similar. The area of 6-gon ABCDEF is S1=248 m², and the diagonal length FA is 28 m. Calculate the area of the 6-gon A'B'C'D'E'F' if F'A' = 36 m. - Mast shadow
 The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines.
The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - A boy
 A boy of 1.7m in height is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff.
A boy of 1.7m in height is standing 30m away from the flagstaff on the same level ground. He observes that the angle of deviation of the top of the flagstaff is 30 degrees. Calculate the height of the flagstaff. - Right angle
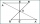 If b=10, c=6, and c are two sides of a triangle ABC, a right angle is at the vertex A, find the value on each unknown side.
If b=10, c=6, and c are two sides of a triangle ABC, a right angle is at the vertex A, find the value on each unknown side. - Median
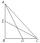 In the ABC triangle is given side a=10 cm and median to side a: ta= 13 cm, and angle gamma 90°. Calculate the length of the median to side b (tb).
In the ABC triangle is given side a=10 cm and median to side a: ta= 13 cm, and angle gamma 90°. Calculate the length of the median to side b (tb). - Calculate 6219
 Right triangle. Given: side b = 15.8 angle alpha = 15° 11`. Calculate the side a, c, beta angle, and area.
Right triangle. Given: side b = 15.8 angle alpha = 15° 11`. Calculate the side a, c, beta angle, and area. - Shadow 73354
 How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long?
How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long? - Calculate: 6679
 In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c
In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c - Ruler
 Peter is looking at John over a ruler that keeps at an arm's distance of 60 cm from the eye, and on the ruler, John measured the height of 15 mm. John is 2 meters high. How far from Peter stands John?
Peter is looking at John over a ruler that keeps at an arm's distance of 60 cm from the eye, and on the ruler, John measured the height of 15 mm. John is 2 meters high. How far from Peter stands John? - Perpendicular 67174
 Calculate the perpendicular s in the right triangle STU (the right angle at the vertex U), if the hypotenuse is long u = 93cm and the perpendicular t = 48 cm
Calculate the perpendicular s in the right triangle STU (the right angle at the vertex U), if the hypotenuse is long u = 93cm and the perpendicular t = 48 cm - Two bodies
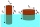 The rectangle with dimensions 8 cm and 4 cm is rotated 360º first around the longer side to form the first body. Then, we similarly rotate the rectangle around the shorter side b to form a second body. Find the ratio of surfaces of the first and second bo
The rectangle with dimensions 8 cm and 4 cm is rotated 360º first around the longer side to form the first body. Then, we similarly rotate the rectangle around the shorter side b to form a second body. Find the ratio of surfaces of the first and second bo - Three parallels
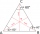 The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle. - Inclined plane
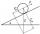 On the inclined plane with an inclination angle of 30°, we will put the body (fixed point) with mass 9 kg. Determine the acceleration of the body motion on an inclined plane.
On the inclined plane with an inclination angle of 30°, we will put the body (fixed point) with mass 9 kg. Determine the acceleration of the body motion on an inclined plane. - Right-angled 81989
 Using Euclid's Theorems and Pythagoras' Theorem, complete the following parameters describing a right-angled triangle ABC with a right angle at vertex C if we know b=10, cb=8
Using Euclid's Theorems and Pythagoras' Theorem, complete the following parameters describing a right-angled triangle ABC with a right angle at vertex C if we know b=10, cb=8 - Measurements of a triangle
 Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft
Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft - The ladder - RT
 The ladder 16 feet reaches up 14 feet on a house wall. The 90-degree angle at the base of the house and wall. What are the other two angles or the length of the leg of the yard?
The ladder 16 feet reaches up 14 feet on a house wall. The 90-degree angle at the base of the house and wall. What are the other two angles or the length of the leg of the yard?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
