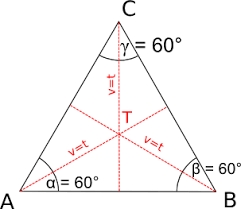
Three parallels
The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebraplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- N points on the side
An equilateral triangle A, B, and C on each of its inner sides lies N=13 points. Find the number of all triangles whose vertices lie at given points on different sides. - Z8–I–5 MO 2019
For eight different points as shown in the figure, points C, D, and E lie on a line parallel to line AB, F is the midpoint of line AD, G is the midpoint of line AC, and H is the intersection of lines AC and BE. The area of triangle BCG is 12 cm² and the - Coordinates
Determine the coordinates of the vertices and the area of the parallelogram, the two sides of which lie on the lines 8x + 3y + 1 = 0, 2x + y-1 = 0, and the diagonal on the line 3x + 2y + 3 = 0 - There
There is a triangle ABC: A (-2,3), B (4, -1), C (2,5). Determine the general equations of the lines on which they lie: a) AB side, b) height to side c, c) Axis of the AB side, d) median ta to side a
- Construct 13581
The vertices of the triangle ABC lie on the circle k. The circle k is divided into three parts in a ratio of 1:2:3. Construct this triangle. - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Semicircles
In a rectangle with sides of 4cm and 8cm, there are two different semicircles, each of which has its endpoints at its adjacent vertices and touches the opposite side. Construct a square such that its two vertices lie on one semicircle, the remaining two o
