Angle practice problems - page 59 of 63
Number of problems found: 1260
- Radians
 Convert 90° to radians. Write the result as a multiple of the number π.
Convert 90° to radians. Write the result as a multiple of the number π. - Quadrilateral ABCD
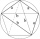 Construct a quadrilateral ABCD if AB = 10cm, AD = 6cm, DC = 6.5cm and angle BCD = 90 degrees.
Construct a quadrilateral ABCD if AB = 10cm, AD = 6cm, DC = 6.5cm and angle BCD = 90 degrees. - Hexagonal pyramid
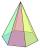 Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm.
Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm. - Diagonals
 Construct a rhombus whose diagonals have lengths of 10cm and 8cm and make an angle of 115°.
Construct a rhombus whose diagonals have lengths of 10cm and 8cm and make an angle of 115°. - ABCDEFGHIJKL 8426
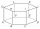 The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees.
The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees. - Goat and circles
 What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle? This task is the mathematical expression of the role of agriculture. The farmer has circular land on which
What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle? This task is the mathematical expression of the role of agriculture. The farmer has circular land on which - Quadrilateral prism
 The body diagonal of a regular quadrilateral prism forms an angle of 60° with the base. The edge of the base is 20 cm long. Calculate the volume of the body.
The body diagonal of a regular quadrilateral prism forms an angle of 60° with the base. The edge of the base is 20 cm long. Calculate the volume of the body. - MO Z8–I–6 2018
 The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line.
The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Calculate 8325
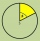 Calculate the area of a circular section given by an angle of 220 degrees if the circle's radius is 20cm. Round the result to cm2
Calculate the area of a circular section given by an angle of 220 degrees if the circle's radius is 20cm. Round the result to cm2 - Arc
 What area of a circle occupied the flowers planted in the arc of a circle with a radius 3 m with a central angle of 45°?
What area of a circle occupied the flowers planted in the arc of a circle with a radius 3 m with a central angle of 45°? - Arc
 The circle arc corresponding to the angle is 357° is 18 dm long. What is the length of the entire circle?
The circle arc corresponding to the angle is 357° is 18 dm long. What is the length of the entire circle? - A kite
 ABCD is a kite. Angle OBC = 20° and angle OCD = 35°. O is the intersection of diagonals. Find angle ABC, angle ADC, and angle BAD.
ABCD is a kite. Angle OBC = 20° and angle OCD = 35°. O is the intersection of diagonals. Find angle ABC, angle ADC, and angle BAD. - Sector
 The perimeter of a circular sector with an angle 0.7 rad is 53 cm. Determine the radius of the circle from which the sector comes.
The perimeter of a circular sector with an angle 0.7 rad is 53 cm. Determine the radius of the circle from which the sector comes. - Circular 72244
 How many kg of grass seed must be bought to start a lawn in the shape of a circular section with a radius of r= 15 m and a central angle of 45 degrees if 1 g of grass seed is used per 1 dm of the square area?
How many kg of grass seed must be bought to start a lawn in the shape of a circular section with a radius of r= 15 m and a central angle of 45 degrees if 1 g of grass seed is used per 1 dm of the square area? - Quadrilateral pyramid
 The regular quadrilateral pyramid has a base edge a = 1.56 dm and a height h = 2.05 dm. Calculate: a) the deviation angle of the sidewall plane from the base plane b) deviation angle of the side edge from the plane of the base
The regular quadrilateral pyramid has a base edge a = 1.56 dm and a height h = 2.05 dm. Calculate: a) the deviation angle of the sidewall plane from the base plane b) deviation angle of the side edge from the plane of the base - Hexagonal pyramid
 Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm.
Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. - Inaccessible direct
 Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B,
Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B, - Children playground
 The playground has a trapezoid shape, and the parallel sides have a length of 36 m and 21 m. The remaining two sides are 14 m long and 16 m long. Find the size of the inner trapezoid angles.
The playground has a trapezoid shape, and the parallel sides have a length of 36 m and 21 m. The remaining two sides are 14 m long and 16 m long. Find the size of the inner trapezoid angles. - Archaeologists 81478
 Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section? - Quadrilateral 8120
 If the pyramid's height is 4 cm and the base area is 16 cm2, include the side edge length of a regular quadrilateral pyramid.
If the pyramid's height is 4 cm and the base area is 16 cm2, include the side edge length of a regular quadrilateral pyramid.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
