Angle practice problems - page 60 of 63
Number of problems found: 1257
- Angle of two lines
There is a regular quadrangular pyramid ABCDV; | AB | = 4 cm; height v = 6 cm. Determine the angles of lines AD and BV. - Length of the arc
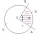What is the arc length of a circle k (S, r=68mm), which belongs to a central angle of 78°? - Irrigation sprinkler
The irrigation sprinkler can twist at an angle of 320° and reach 12 meters. Which area can you irrigate? - Arc
The length of the circle is 13, and the arc length of the circle is 5. What is the magnitude of the angle of this arc? - Quadrant II
Calculate the radius of the quadrant, which area is equal to the area of the circle with radius r = 15 cm. - Quarter circular
The wire hooked around the perimeter of the quarter-circular arc has a length of 14π+56. Determine the radius of the circle arc. - The central
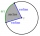The central angle of a sector is 30°, and the radius is 15 m. Determine its perimeter. - Three vectors
The three forces whose amplitudes are in ratio 9:10:17 act in the plane at one point to balance. Determine the angles of each of the two forces. - Calculate deltoid
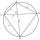Calculate the diagonals in the deltoid with sides of 10, 10, and shorter 6, 6 cm. - Circle arc
Calculate the circular arc area in m² where the diameter is 263 dm and the central angle is 40°. Please result round to three decimal places. - Interior angles
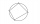In a quadrilateral ABCD, whose vertices lie on some circle, the angle at vertex A is 58 degrees, and the angle at vertex B is 134 degrees. Calculate the sizes of the remaining interior angles. - The chord
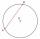A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°? - Circle sector
The circular sector with a central angle 160° has an area 452 cm². Calculate its radius r. - Hexa pyramid
The base of the regular pyramid is a hexagon, which can be described as a circle with a radius of 2 m. Find the volume of the pyramid to be 2.5 m high. - The tower
The tower of the Dean's Church in Ústí nad Labem deviates from the original vertical axis by 220 cm. Its original height was 48 m. At what height is the highest point of this tower now? Enter the result to the nearest centimeter. - Circular segment
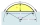A circular segment has an area of 6.04 cm², the central omega angle is 15 degrees, what is the radius? - Rectangular trapezoid
The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid. - Arc-sector
arc length = 17 cm area of sector = 55 cm² arc angle = ? the radius of the sector = ? - Quadrilateral 8405
Calculate the magnitude of the largest inner angle and the deviation of the diagonals in the quadrilateral, whose vertices correspond to points 1, 5, 8, and 12 on the dial. - Annulus
Two concentric circles with radii 1 and 9 surround the annular circle. This ring is inscribed with n circles that do not overlap. Determine the highest possible value of n.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
