Examples of area of plane shapes - page 25 of 131

Number of problems found: 2604

Dimensions - rectangle
One side of the rectangle is 12 cm longer than the other. If we reduce each dimension by a third, the area of the rectangle will be reduced by 60 cm². Determine the dimensions of the rectangle.
Right-angled - legs
The lengths of legs are a = 7.2 cm and b = 10.4 cm in the right-angled triangle ABC. Calculate: a) lengths of the sections of the hypotenuse b) height to the hypotenuse c
The area 2
The area of a rectangular piece of tablecloth is 3/4 m². Its width is 3/10 m. What is its length?
Parallelogram - sides
A parallelogram has a perimeter of 30 cm and heights of 10 cm and 6 cm. Find the lengths of its sides.
Rectangle - area and width
The length of the rectangle is 1 cm more than its width. Its area is 4 cm². What is its width?
The length 11
The length of a rectangle is four times its width. If the area is 100 m², what is the length of the rectangle?
Inscribed circle
A circle is inscribed in the triangle with sides of 13 cm, 14 cm, and 15 cm. What is its radius?
A pressure
How much compressive force does an aquarium with a bottom area of 0.24 m² exert on the table when a pressure of 3 kPa is created?
Rectangles - integers
How many different rectangles with integer side lengths have an area S = 60 cm²?
Isosceles trapezoid
Find the area of an isosceles trapezoid with bases of 8cm and 72mm. The height of the trapezoid is equal to three-quarters of the longer base.
Isosceles trapezoid
Find the area of an isosceles trapezoid; if the bases are 12 cm and 20 cm, the arm's length is 16 cm.
The playground
The playground is a square with a side of 64 m. It is fenced on three sides. What is the playground area, and how long is the fence?
Percent change
The length of a rectangle is increased by 25%, and the width is decreased by 10%. By what percent is the area of the rectangle larger than the area of the original rectangle?
Diagonals of pentagon
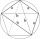Calculate the diagonal length of the regular pentagon: a) inscribed in a circle of radius 12dm; b) a circumscribed circle with a radius of 12dm.
Sss triangle
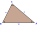Calculate the area and heights in the triangle ABC by sides a = 8cm, b = 11cm, c = 12cm
Around
Around the circular flowerbed with a radius of 2 m is a sidewalk 80 cm wide. How many square meters does the sidewalk have?
Trapezoid - sides
Calculate the unknown side and the area of the ABCD trapezoid if you know: side a = 7.5 side b = 3.6 side d = 4.4 height v = 3.4 circumference o = 19 c =? S =?
Right-angled triangle
Determine the area of a right triangle whose side lengths form successive members of an arithmetic progression, and the radius of the circle described by the triangle is 5 cm.
Trapezoid MO-5-Z8
Trapezoid KLMN has bases 12 and 4 cm long. The area of triangle KMN is 9 cm². What is the area of the trapezoid KLMN?
Circular ring
A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form.

Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.