Combinatorics - math word problems - page 46 of 55
Number of problems found: 1085
- The triangle 5
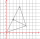The triangle below has vertices A(-1,-2), B(2,2), and C(-1,4). What is the area of △ABCin square coordinate units? - Probability of malaria
A survey carried out at a certain hospital indicates that the probability that a patient testing positive for malaria is 0.6. What is the probability that two patients were selected at random (i) one is negative while the other tested positive (i) both pa - Probability
In the election, 2400000 voters out of a total of 6000000 voters voted for party Z. Let us randomly select three voters and consider the random variable ξ={number of voters of party Z in the sample of three voters}. Determine a) the probability distributi - Crime solving probability
The police solved 21 crimes in the monitored period. The probability of solving a crime is 0.64. What is the probability that the police: a) just solved 7 crimes b) did not solve at least 2 criminal offenses P.S. Let's assume ideal police officers - Product 3DN
How many three-digit numbers are there whose product of digits is 5? - Multiple-choice
A multiple-choice test consists of 4 questions. Each question has three different answers, with only one answer being correct. Each question is answered randomly by one student. Determine the expected value for the number of correct answers that the stude - Sample Proportion
In a California community college, 60% of students will transfer to a college in the CSU system. The number of students in a sample who will transfer follows a binomial distribution. Four hundred students are randomly selected from the college, and 224 of - Genetic disease
One genetic disease was tested positive in both parents of one family. It has been known that any child in this family has a 25% risk of inheriting the disease. A family has three children. What is the probability of this family having one child who inher - Heptagon triangle probability
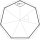We randomly select three different points from the vertices of a regular heptagon and connect them with line segments. The probability that the resulting triangle will be isosceles is equal to: (A) 1/3 (B) 2/5 (C) 3/5 (D) 4/7 - Component deviation probability There are 200 components in the production batch, of which 26 have a plus deviation from the nominal value. Calculate the probability that none of the 10 products selected will have a positive variance if we make selections without repetition
- Lifespan
The lifetime of a light bulb is a random variable with a normal distribution of x = 300 hours, σ = 35 hours. a) What is the probability that a randomly selected light bulb will have a lifespan of more than 320 hours? b) To what value of L hours can the la - An exam - normal distribution
Five thousand students take an exam with a mean of 59 and a deviation of 8. How many students will score less than 75? - Triangles
Five sticks with a length of 2,3,4,5,6 cm. How many ways can you choose three sticks to form three sides of a triangle? - Crimson Lynx
Captain Emily has a ship, the H. M. S Crimson Lynx. The ship is five furlongs from the dread pirate Umaima and her merciless band of thieves. If her ship hasn't already been hit, Captain Emily has a probability of 3/5 of hitting the pirate ship. If her sh - Isosceles triangle construction
There are six lines 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, and 9 cm long, two of each length. How many isosceles triangles can be constructed from them? List all options. - Product quality
We have three series of products. We select one product for quality control. Determine the probability of finding a low-quality product if the first batch contains 2/3, the second batch 7/9, and the third batch 3/4 quality products. - Bernoulli distribution The production of solar cells produces 2% of defective cells. Assume the cells are independent and that a lot contains 800 cells. Approximate the probability that less than 20 cells are defective. (Answer to the nearest three decimals).
- Families 2
Seven hundred twenty-nine families have six children each. The probability of a girl is 1/3, and the likelihood of a boy is 2/3. Find the number of families having two girls and four boys. - Dice Rolling Six Probability
Three players roll the dice. They can start the game when a six is rolled. Everyone rolls 1 time. a) What is the probability that exactly one starts in the first round? b) What is the probability that at least two start? - Six segmants
Given are 6 line segments with lengths of 3 cm, 4 cm, 5 cm, 7 cm, 8 cm, and 9 cm. How many equilateral triangles can make from them? List all the options.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
