Cylinder practice problems - page 22 of 24
Number of problems found: 480
- The largest
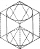We cut the largest possible cylinder from a 20 cm cube. What is the volume of this cylinder? - Quadrilateral 23891
A cylinder with the maximum possible base was ground from a wooden regular quadrilateral prism (edge 2.8 cm, height 7.5 cm). What percentage of the material was wasted as waste? What percentage would it be if the height of the prism were twice as large? - The pot
The pot is in 1/3 filled with water. The bottom of the pot has an area of 329 cm². How many centimeters rise in water level in the pot after adding 1.2 liters of water? - Reinforcement 42491
The concrete ring (used for reinforcement in wells) has an inner diameter of 800 mm and an outer diameter of 900 mm. It is made of concrete with a density of 2,500 kg/m³. Its height is 1 m. Calculate its mass. - Equilateral cylinder
The equilateral cylinder (height = base diameter; h = 2r) has a V = 178 cm³ volume. Calculate the surface area of the cylinder. - Triangular prism
The curved part of the rotating cylinder is four times larger than the area of its base. Determine the volume of the regular triangular prism inscribed in the cylinder. The radius of the bottom of the cylinder is 10 cm. - Cylinder-shaped 4410
A cylinder-shaped case is to be made for a ruler with the shape of a prism with a base in the shape of an equilateral triangle with a side length of 3 cm. What must be the smallest inner diameter of the housing? Determine the size to the nearest tenth of - Surrounded 8283
The cube has an edge length of 5 cm. This cube surrounds a rotating cylinder. Find the surface area of the shell and the volume of the cylinder. - Cylinder - h
The cylinder volume is 140 cm³. The base radius is 7 cm. Calculate the height of the cylinder. - Container NDR
A cone-shaped container with a bottom diameter of 60 cm and a side length of 0.5 m is filled with water. We pour the water into a container with the face of a cylinder with a radius of 3dm and a height of 20cm. Will the cylinder overflow or not be complet - Equilateral cylinder
A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere. - Cube into cylinder
If we dip a wooden cube into a barrel with a 40cm radius, the water will rise 10 cm. What is the size of the cube edge? - Surface area of cylinder
Determine the lateral surface of the rotary cylinder, which is a circumscribed cube with a 5 cm edge length. - Surface of the cylinder
Calculate the cylinder's surface area when its volume is 45 l, and the base's perimeter is three times the height. - Wood floats
A wooden cylinder with a diameter of 20 cm and a length of 1 m is immersed in water. The specific weight of wood is 700kg/m³. For example, calculate the height of the wood that is above the water. The role was assigned to me as a high school freshman math - Diameter 7648
The mug has the shape of a cylinder with a height of 60.7 mm. There is two dl of water in it. If we dip a ball with a diameter of 40 cm into the water, the water will not overflow. What is the minimum diameter of the cup? - Cylindrical 5890
A cylindrical mug is packed in a 1-liter cube paper box. The mug is in close contact with all the walls of the cube. What volume is my mug? - Inscribed 6155
A cylinder with a height equal to half the height of the cone is inscribed in the rotating cone. Find the volume ratio of both bodies. - Cylindrical 66744
How many liters will fit in a cylindrical container with a base area of 0.06 m² and a height of 5 cm? - Revolutions of cylinder
The rotating cone has a volume of 120 dm³. How tall is a cylinder of revolution with the same volume as a cone of revolution?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
