Triangular prism

The curved part of the rotating cylinder is four times larger than the area of its base. Determine the volume of the regular triangular prism inscribed in the cylinder. The radius of the bottom of the cylinder is 10 cm.

Your answer:

Help us improve! If you spot a mistake, please let let us know. Thank you!

Tips for related online calculators

See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

algebra

rearrange variables

arithmetic

square root

solid geometry

cylinder

planimetry

Pythagorean theorem
right triangle
circle
area of a shape
triangle

Units of physical quantities

volume

Grade of the word problem

practice for 13 year olds
practice for 14 year olds

We encourage you to watch this tutorial video on this math problem: video1 video2

Related math problems and questions:

Wooden prism
Find the mass of a regular triangular prism made of oak, whose height equals the perimeter of its equilateral triangular base, and whose base is inscribed in a circle with radius 6.M cm (where M is the month of your birth). The density of oak is 680 kg/m³
Cylinder - curved area
The curved area of the rotary cylinder is three times greater than the area of one base of this cylinder. The radius of the base of the cylinder is 10 cm. What is the surface area of the cylinder?
A prism
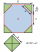A prism with an altitude of 15 cm has a base in the form of a regular octagon inscribed in a square of 10 cm x 10 cm. Find the volume of the prism.
Circumscribed hexa prism
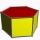The regular hexagonal prism is 2 cm high. The radius of the circle circumscribed by the base is 8 cm. Determine its volume and surface.
Triangular prism - regular
The regular triangular prism is 7 cm high. Its base is an equilateral triangle whose height is 3 cm. Calculate the surface and volume of this prism.
Tetrahedron water level
A container shaped like a rotating cylinder with a base radius of 5 cm is filled with water. If a regular tetrahedron with an edge of 7 cm is immersed in it, how much will the water level in the container rise?
The regular
The regular triangular prism has a base in the shape of an isosceles triangle with a base of 86 mm and 6.4 cm arms; the height of the prism is 24 cm. Calculate its volume.