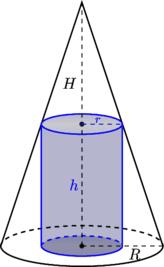
Inscribed 6155
A cylinder with a height equal to half the height of the cone is inscribed in the rotating cone. Find the volume ratio of both bodies.
Final Answer:
Showing 1 comment:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cone
Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder. - Equilateral cylinder
A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere. - Rotary bodies
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area? - 10-centimeter-high 7638
A block with a square base is inserted into a 10-centimeter-high cylinder in such a way that its base is inscribed in the base of the cylinder. The edge of the base of the block measures 4 cm. Both bodies have the same height. Calculate the difference bet - Cone in cylinder
The cylinder is an inscribed cone. Find the ratio of the volume of the cone and cylinder. Please write the ratio as a decimal number and as a percentage. - Equilateral 81222
A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere? - Volume ratio
Calculate the volume ratio of balls circumscribed (diameter r) and inscribed (diameter ϱ) into an equilateral rotating cone.
