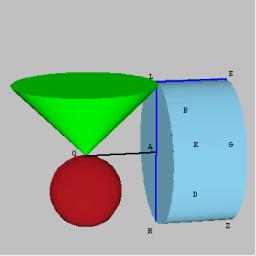
Cone
Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder.
Your answer:
Your answer:
You need to know the following knowledge to solve this word math problem:
solid geometrybasic operations and conceptsGrade of the word problem
Related math problems and questions:
- Cylinder in Cone Volume
A cylinder with a height equal to half the height of the cone is inscribed in the rotating cone. Find the volume ratio of both bodies. - Volume ratio
Calculate the volume ratio of balls circumscribed (diameter r) and inscribed (diameter ϱ) into an equilateral rotating cone. - Cylindrical container
An open-topped cylindrical container has a volume of V = 3140 cm³. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container. - Sphere in cone
A sphere of radius 3 cm describes a cone with minimum volume. Determine the cone's dimensions. - Cross-sections of a cone
Cone with base radius 15 cm and height 20 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Cone area and side
Calculate a rotating cone's surface area and volume with a height of 1.25 dm and 17,8 dm side. - Triangular prism
The curved part of the rotating cylinder is four times larger than the area of its base. Determine the volume of the regular triangular prism inscribed in the cylinder. The radius of the bottom of the cylinder is 10 cm.
