Kužel
Do rotačního kužele o rozměrech r = 8 cm, v = 8 cm vepište válec maximálního objemu tak, aby osa válce byla kolmá na osu kužele. Určete rozměry válce.
Vaše odpověď:
Vaše odpověď:
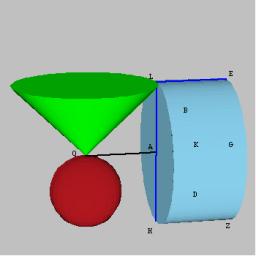
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
stereometriezákladní operace a pojmyÚroveň náročnosti úkolu
Související a podobné příklady:
- Do rotačního
Do rotačního kužele je vepsán válec, jehož výska je rovna polovině výšky kužele. Určete poměr objemů obou těles. - Z obdélníku
Z obdélníku o rozměrech 6 cm a 4 cm jsme svinuli plášť rotačního válce o výšce 4 cm. Určete objem válce. - Obvod podstavy
Obvod podstavy rotačního válce je tak velký jako jeho výška. Jaký je průměr a výška válce o objemu 1 litr? - Koule a kužel
Do koule o poloměru G = 36 cm vepište kužel s největším objemem. Jaký je tento objem a jaké jsou rozměry kužele? - Nádoba tvaru válce
Nahoru otevřená nádoba tvaru válce má objem V = 3140 cm³. Určitě rozměry válce (r, v) tak, aby na vytvoření této nádoby se minulo nejméně materiálu. - Kužel ve válci
Do válce je vepsán kužel. Určite poměr objemu kužele a válce. Poměr vyjádřete jako desetinné číslo a i jako procento. - Válec
Vypočítejte vnitřní rozměry nádoby tvaru rotačního válce, jejíž objem je 26 l, pokud se výška nádoby rovná průměru podstavy.
