Maximum - příklady
Pokyny: Vyřešte každý úkol pečlivě a ukažte své celé řešení. Pokud je to vhodné, proveďte zkoušku správnosti řešení.Počet nalezených příkladů: 80
- Rámař
 Rámař má připravit 23 kusů rámečků na obrázky. Rámeček bude mít rozměry 30 cm a 42 cm. Lišty, ze kterých bude rámečky dělat, mají délku 3 metry. a) Kolik rámečků udělá z jedné lišty? b) Kolik lišt bude potřebovat?
Rámař má připravit 23 kusů rámečků na obrázky. Rámeček bude mít rozměry 30 cm a 42 cm. Lišty, ze kterých bude rámečky dělat, mají délku 3 metry. a) Kolik rámečků udělá z jedné lišty? b) Kolik lišt bude potřebovat? - Na přímce 3
 Na přímce p: 2x + y + 1 = 0 najděte bod A ∈ p, který je nejblíže bodu P =(1,0)
Na přímce p: 2x + y + 1 = 0 najděte bod A ∈ p, který je nejblíže bodu P =(1,0) - Jirka 5
 Jirka si vyjel na mopedu na třídenní výlet. První den ujel 90 km, druhý den 30 km a třetí den 60 km. Jel vždy stejnou průměrnou rychlosti a vždy celý počet hodin. Vypočtěte průměrnou rychlost, jestliže Jirka jel největší možnou rychlostí.
Jirka si vyjel na mopedu na třídenní výlet. První den ujel 90 km, druhý den 30 km a třetí den 60 km. Jel vždy stejnou průměrnou rychlosti a vždy celý počet hodin. Vypočtěte průměrnou rychlost, jestliže Jirka jel největší možnou rychlostí. - Rozsah tříd seskupených údajů
 Ve třídách seskupených údajů, jako jsou 10-15, 16-20, 21-25, 26-30 s příslušnými frekvencemi každé třídy jako 3, 5, 4, 3, pak rozsah (variační rozpětí) je: a. 15 b. 6 c. 20 d. 5
Ve třídách seskupených údajů, jako jsou 10-15, 16-20, 21-25, 26-30 s příslušnými frekvencemi každé třídy jako 3, 5, 4, 3, pak rozsah (variační rozpětí) je: a. 15 b. 6 c. 20 d. 5 - Do kruhu
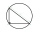 Do kruhu s průměrem 20cm byl vepsán pravoúhlý trojúhelník, jehož přepona je průměrem kruhu má co největší obsah. Vypočítej obsah tohoto trojúhelníku.
Do kruhu s průměrem 20cm byl vepsán pravoúhlý trojúhelník, jehož přepona je průměrem kruhu má co největší obsah. Vypočítej obsah tohoto trojúhelníku. - Odlehlé hodnoty
 Učitel zjistil, že pět číselné shrnutí souboru dat (tj. minimum, spodní kvartil, medián, horní kvartil, maximum) je: 0, 5, 7, 14, 17 Pozorování se považuje za odlehlou hodnotu (outlier), je-li níže: Pozorování se považuje za odlehlou hodnotu (outlier), je
Učitel zjistil, že pět číselné shrnutí souboru dat (tj. minimum, spodní kvartil, medián, horní kvartil, maximum) je: 0, 5, 7, 14, 17 Pozorování se považuje za odlehlou hodnotu (outlier), je-li níže: Pozorování se považuje za odlehlou hodnotu (outlier), je - Tangens a derivace
 Funkce: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Najít; i) vertikální a horizontální asymptoty iii) intervaly poklesu a růstu iii) Místní maxima a místní minima iv) interval konkávnosti a inflexe. A načrtněte graf.
Funkce: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Najít; i) vertikální a horizontální asymptoty iii) intervaly poklesu a růstu iii) Místní maxima a místní minima iv) interval konkávnosti a inflexe. A načrtněte graf. - Test obsahoval
 Test obsahoval 50 otázek, na každou otázku byla možná jedna správná odpověď. Výsledek testu je dán součtem správných odpovědí, maximum 100 bodů. Kritériem pro přijetí bylo dosažení 50 bodů. Uchazeč o studium zodpověděl správně 36 otázek. Kolik bodů dostal
Test obsahoval 50 otázek, na každou otázku byla možná jedna správná odpověď. Výsledek testu je dán součtem správných odpovědí, maximum 100 bodů. Kritériem pro přijetí bylo dosažení 50 bodů. Uchazeč o studium zodpověděl správně 36 otázek. Kolik bodů dostal - Poplatek za úvěr
 Rodina Nováková si vzala z banky úvěr (půjčku) 120 000 eur. Jaká byla výše poplatku za zpracování, zřízení a poskytnutí úvěru, pokud podle sazebníku poplatků banky je jeho výše 0,80% z objemu úvěru, minimálně však 250eur a maximálně 950eur?
Rodina Nováková si vzala z banky úvěr (půjčku) 120 000 eur. Jaká byla výše poplatku za zpracování, zřízení a poskytnutí úvěru, pokud podle sazebníku poplatků banky je jeho výše 0,80% z objemu úvěru, minimálně však 250eur a maximálně 950eur? - Trojúhelník - pravoúhlý
 Základna pravoúhlého trojúhelníku je 10 centimetrů a nejdelší strana má 26 centimetrů. Jaká je plocha trojúhelníku?
Základna pravoúhlého trojúhelníku je 10 centimetrů a nejdelší strana má 26 centimetrů. Jaká je plocha trojúhelníku? - Statistika výrobních společností
 Náhodný vzorek 8 výrobních společností se vybere z populace výrobních společností. Tržní hodnoty (v milionech randov) těchto osmi výrobních společností jsou: 17 65 117 206 172 181 221 94 Jaká je nejnižší a nejvyšší tržní hodnota? Najděte průměr. Nakreslet
Náhodný vzorek 8 výrobních společností se vybere z populace výrobních společností. Tržní hodnoty (v milionech randov) těchto osmi výrobních společností jsou: 17 65 117 206 172 181 221 94 Jaká je nejnižší a nejvyšší tržní hodnota? Najděte průměr. Nakreslet - Výroba náhrdelníků
 V továrně na šperky vyrábějí tři montážníci korálkové náhrdelníky. Marcus dokáže vyrobit 22 náhrdelníků za hodinu po celý den. Anita dokáže vyrobit 25 náhrdelníků během prvních tří hodin dne a poté zpomalí na 16 náhrdelníků na zbytek dne. Yara dokáže vyro
V továrně na šperky vyrábějí tři montážníci korálkové náhrdelníky. Marcus dokáže vyrobit 22 náhrdelníků za hodinu po celý den. Anita dokáže vyrobit 25 náhrdelníků během prvních tří hodin dne a poté zpomalí na 16 náhrdelníků na zbytek dne. Yara dokáže vyro - Na louce
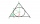 Na louce přistála kosmická loď ve tvaru koule o průměru 6 m. Aby nepoutala pozornost, zakryli ji marťanci střechou ve tvaru pravidelného kužele. Jak vysoká bude tato střecha, aby spotřeba krytiny byla minimální?
Na louce přistála kosmická loď ve tvaru koule o průměru 6 m. Aby nepoutala pozornost, zakryli ji marťanci střechou ve tvaru pravidelného kužele. Jak vysoká bude tato střecha, aby spotřeba krytiny byla minimální? - Megapizza
 Megapizza bude rozdělena mezi 100 lidí. 1. dostane 1%, 2. 2% ze zbytku, 3. 3% ze zbytku atd. Poslední 100. 100% ze zbytku. Který člověk dostal největší porci?
Megapizza bude rozdělena mezi 100 lidí. 1. dostane 1%, 2. 2% ze zbytku, 3. 3% ze zbytku atd. Poslední 100. 100% ze zbytku. Který člověk dostal největší porci? - Ze železné
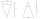 Ze železné tyče ve tvaru hranolu o rozměrech 5,6 cm 4,8 cm, 7,2 cm je třeba vyrobit co největší kužel. a) Vypočtěte jeho objem. b) Vypočtěte odpad.
Ze železné tyče ve tvaru hranolu o rozměrech 5,6 cm 4,8 cm, 7,2 cm je třeba vyrobit co největší kužel. a) Vypočtěte jeho objem. b) Vypočtěte odpad. - Měření - statistika
 V měření 63 žáků byly zjištěny následující údaje o výši a příslušném počtu žáků: výška; počet žáků 159cm; 1 161cm; 1 162cm; 2 163cm; 1 164cm; 2 165cm; 2 166cm; 3 167cm; 2 168cm; 4 169cm; 3 170cm; 5 171cm; 6 172cm; 7 173cm; 9 174cm; 5 175cm; 2 177cm; 1 178
V měření 63 žáků byly zjištěny následující údaje o výši a příslušném počtu žáků: výška; počet žáků 159cm; 1 161cm; 1 162cm; 2 163cm; 1 164cm; 2 165cm; 2 166cm; 3 167cm; 2 168cm; 4 169cm; 3 170cm; 5 171cm; 6 172cm; 7 173cm; 9 174cm; 5 175cm; 2 177cm; 1 178 - Obsah kosočtverce
 Který kosočtverec se stranou dlouhou 7,5 cm má: a/největší obsah, b/nejmenší obsah
Který kosočtverec se stranou dlouhou 7,5 cm má: a/největší obsah, b/nejmenší obsah - Plášť 8
 Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální?
Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální? - Střelec 4
 Střelec střílí do terče, přičemž předpokládáme, že jednotlivé výstřely jsou navzájem nezávislé a pravděpodobnost zásahu je u každého z nich 0,2. Střelec střílí tak dlouho, dokud poprvé terč nezasáhne, poté střelbu ukončí. (a) Jaký je nejpravděpodobnější p
Střelec střílí do terče, přičemž předpokládáme, že jednotlivé výstřely jsou navzájem nezávislé a pravděpodobnost zásahu je u každého z nich 0,2. Střelec střílí tak dlouho, dokud poprvé terč nezasáhne, poté střelbu ukončí. (a) Jaký je nejpravděpodobnější p - Derivační problém
 Součet dvou čísel je 12. Najděte tato čísla, jestliže: a) Součet jejich třetích mocnin je minimální. b) Součin jednoho s třetí mocninou druhého je maximální. c) Obě jsou kladná a součin jednoho s druhou mocninou druhého je maximální.
Součet dvou čísel je 12. Najděte tato čísla, jestliže: a) Součet jejich třetích mocnin je minimální. b) Součin jednoho s třetí mocninou druhého je maximální. c) Obě jsou kladná a součin jednoho s druhou mocninou druhého je maximální.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
