Grade - math word problems - page 212 of 950
Number of problems found: 18982
- The midpoint 2
Find the value of x if M is the midpoint of PQ, PQ=10x−7, and PM=14. - Sequence:
Sequence: 4,10,40,400,16,000,______, ________ Find these two members. - Nicolette
Nicolette makes a small bead bracelet using five red, eight purple, and six green beads. A large necklace has the same ratio of beads as a small bracelet. If the large necklace requires 15 red beads, how many purple beads are needed to make a large bracel - Solve 15
Solve equation with fractions 29/12=24/12+?/12 - Convert 4 Convert 2 7/10 into an improper fraction.
- A town 2
A town has raised 3/8 of the 12,000 and needs to furnish its new library. How much more money is it hoping to raise? - A solution
A solution of salt and water has 15% salt by weight. From it, 30 kg evaporated, and the solution now contains 20% salt. Find the original quantity of the solution. - Express 66
Express 6 whole 7/10 hours in minutes. - Adding 11
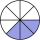You are adding numbers. Which of the following numbers to 3/5 will give a whole number? a. 2 b. 2/5 c. 5/3 d. 3/5 - Year salary
2/5 of a man's salary is 40,000. What is his salary? - Fencing
Ruby is purchasing fencing to go around a rectangular lot which is 4x + 9 feet long and 3x - 5 feet wide. Which expression represents the amount of fencing she must buy? - Two drops
Between 5:00 pm to 6:00 pm, the temperature dropped 3°C. Between 6:00 pm to 7:00 pm, the temperature dropped 4°C. What was the total drop in temperature from 5:00 pm to 7:00 pm? - Expression with powers Which expression is equivalent to 2.1 raised to the fifth power divided by 0.9 raised to the fourth power, all raised to the third power?
- Marbles 4
Sipho has a cylindrical tank with a radius of 8cm and a height of 10cm. The bottom of the tank is filled with marbles, and the tank is then filled with water to a height of 6,4 cm. When the marbles are removed, the water level drops to 4cm. Using the info - Temp drop
It is 70°F , and the temperature is expected to drop to 85° in the next month. What is the temperature expected to be? - Carbohydrates
Suppose five pieces of candy contain 11 grams of carbohydrates. How many grams of carbohydrates do 20 pieces contain? - Sarah 2
Sarah noticed that the temperature went from 20 degrees and dropped to -10 degrees. Sarah says that the change in temperature is -30 degrees, while her friend Kenya says that the temperature change is 10 degrees. Who is correct? Explain your reasoning - Full of water
A man removed 2/7 of a tank full of water. If it now contains 450 liters, how many liters does it hold when full? - Angles in a triangle
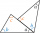In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle? - Conversion 77474
A wooden prism is 220 cm long, 10 cm high, and 10 cm wide. What is the conversion of its volume to m³?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
