Examples for secondary school students - page 19 of 232
Number of problems found: 4622
- Three dice 2
 What is the probability that two odd numbers will be the same when three dice are rolled?
What is the probability that two odd numbers will be the same when three dice are rolled? - In class 24
 There are a total of 16 students in the class, a quarter of whom are girls. We randomly select a team of five. Determine the probability that the team will have: a) at least 4 girls. b) at most 1 girl. c) no girls.
There are a total of 16 students in the class, a quarter of whom are girls. We randomly select a team of five. Determine the probability that the team will have: a) at least 4 girls. b) at most 1 girl. c) no girls. - In a regular 5
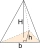 In a regular triangular prism ABCV, the deviation of the side wall and the base plane is α = 45°. Determine the deviation of the side edge and the base plane.
In a regular triangular prism ABCV, the deviation of the side wall and the base plane is α = 45°. Determine the deviation of the side edge and the base plane. - Christmas 4
 There are only 3 packages left under the tree - two for Julka and one for Zuzka. Julka took two at once. What is the probability that both belong to her?
There are only 3 packages left under the tree - two for Julka and one for Zuzka. Julka took two at once. What is the probability that both belong to her? - How many 172
 How many five-digit numbers are there that have exactly 2 fours and exactly 3 sevens in their notation?
How many five-digit numbers are there that have exactly 2 fours and exactly 3 sevens in their notation? - Between terminals
 Between terminals of a 220V resistor. A current of 220mA flows through the resistor. Determine the current that flows through the resistor if we connect it to the terminal of a 24 V voltage source.
Between terminals of a 220V resistor. A current of 220mA flows through the resistor. Determine the current that flows through the resistor if we connect it to the terminal of a 24 V voltage source. - The tower
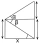 From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower?
From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower? - HAMMER 4
 Determine how many ways can the letters of the word HAMMER be rearranged so that in this rearrangement some group of consecutive letters forms the word CAL.
Determine how many ways can the letters of the word HAMMER be rearranged so that in this rearrangement some group of consecutive letters forms the word CAL. - On a mass
 The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make.
The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make. - Area 51
 The area of the triangle is 54.39, alpha is 32 °, and gamma is 144 °.
The area of the triangle is 54.39, alpha is 32 °, and gamma is 144 °. - Gardener 5
 The gardener bought 17 apple trees and 11 pears. He paid a total of €111.65. How many euros did 1 pear cost, if we know that its price was 35 cents higher than the price of 1 apple tree? How much would the gardener pay for 28 apple trees and 15 pears?
The gardener bought 17 apple trees and 11 pears. He paid a total of €111.65. How many euros did 1 pear cost, if we know that its price was 35 cents higher than the price of 1 apple tree? How much would the gardener pay for 28 apple trees and 15 pears? - Determine the surface area
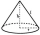 Find the surface area of a cone of height 30 cm whose side makes an angle of 60° with the base plane.
Find the surface area of a cone of height 30 cm whose side makes an angle of 60° with the base plane. - Quadrilateral - irregular
 Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees - Unit circle
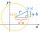 In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A.
In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - X-ray intensity
 The intensity of X-ray radiation is reduced by half when passing through a 13.5 mm thick lead layer. Determine the thickness of the lead plate that will reduce the radiation intensity to one tenth of the original value. If we know that the intensity decre
The intensity of X-ray radiation is reduced by half when passing through a 13.5 mm thick lead layer. Determine the thickness of the lead plate that will reduce the radiation intensity to one tenth of the original value. If we know that the intensity decre - Equation - integers
 Solve the equation with the unknown x from the field of natural numbers 1+6+11+16+. ... +x=970
Solve the equation with the unknown x from the field of natural numbers 1+6+11+16+. ... +x=970 - Rows of chairs
 There are 15 chairs in the first row. There are 3 more chairs in each row. How many chairs are there in the first 20 rows?
There are 15 chairs in the first row. There are 3 more chairs in each row. How many chairs are there in the first 20 rows? - Penny and rolls
 For a hundred crowns I have to buy a hundred pieces of pastry at the prices of rolls of 0.50 crowns, bread 10 crowns, and a roll of 3 crowns. How much of what should I buy? (The Slovak koruna was the currency in Slovakia before the euro or the Czech korun
For a hundred crowns I have to buy a hundred pieces of pastry at the prices of rolls of 0.50 crowns, bread 10 crowns, and a roll of 3 crowns. How much of what should I buy? (The Slovak koruna was the currency in Slovakia before the euro or the Czech korun - In a football
 In a football tournament of eight teams, where each team played each other exactly once, points were awarded as follows: the winner of the match received 3 points, the loser received 0 points, and in the event of a draw, each team received 1 point. At the
In a football tournament of eight teams, where each team played each other exactly once, points were awarded as follows: the winner of the match received 3 points, the loser received 0 points, and in the event of a draw, each team received 1 point. At the - Traffic accidents
 Of the total number of traffic accidents, 80% occur in the village and 20% outside the village. If the number of traffic accidents in the village were reduced by 40%, by what percentage would the total number of traffic accidents decrease?
Of the total number of traffic accidents, 80% occur in the village and 20% outside the village. If the number of traffic accidents in the village were reduced by 40%, by what percentage would the total number of traffic accidents decrease?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
