Examples for secondary school students - page 45 of 231
Number of problems found: 4614
- Mr. Cruz
 Mr. Cruz borrowed 21,600 euros for three years at 16 2⁄3% compounded annually. At the same time, Mr. Santos borrowed the same Amount at Simple Interest for the same period and at the same interest rate. Who Pays more and how much?
Mr. Cruz borrowed 21,600 euros for three years at 16 2⁄3% compounded annually. At the same time, Mr. Santos borrowed the same Amount at Simple Interest for the same period and at the same interest rate. Who Pays more and how much? - Two alloys
 Two alloys, Y and Z, are each made up of zinc, tin, and copper. In alloy Y, the ratio of zinc to tin is 2:5, and the ratio of copper to tin is 4:3. Find the ratio of copper:zinc:tin in alloy Y.
Two alloys, Y and Z, are each made up of zinc, tin, and copper. In alloy Y, the ratio of zinc to tin is 2:5, and the ratio of copper to tin is 4:3. Find the ratio of copper:zinc:tin in alloy Y. - Monthly savings account
 I will deposit CZK 1,500 into my savings account every month. After ten years, what will be in the account if the interest rate is 4%, the interest period is one month, and the interest tax is 15%?
I will deposit CZK 1,500 into my savings account every month. After ten years, what will be in the account if the interest rate is 4%, the interest period is one month, and the interest tax is 15%? - Second prize
 Jamie and Mark each bought a raffle ticket to win a new laptop or a new cell phone, where only 125 tickets were told. The first ticket holder wins the prize of their choice and is removed from the drawing. The holder of the second ticket drawn wins the re
Jamie and Mark each bought a raffle ticket to win a new laptop or a new cell phone, where only 125 tickets were told. The first ticket holder wins the prize of their choice and is removed from the drawing. The holder of the second ticket drawn wins the re - Apple pear division
 How many ways can you divide two identical apples and: a) 3, b) 4, c) 5 identical pears between Janka and Mařenka?
How many ways can you divide two identical apples and: a) 3, b) 4, c) 5 identical pears between Janka and Mařenka? - Operation expression value
 The operation ♤ is defined by the relation A ♤ B = AB - A - B. What is the value of the expression 5 ♤ (4 ♤ 3) equal to?
The operation ♤ is defined by the relation A ♤ B = AB - A - B. What is the value of the expression 5 ♤ (4 ♤ 3) equal to? - Card number probability
 On ten identical cards, there are numbers from zero to nine. Determine the probability that a two-digit number randomly drawn from the given cards is: a) even b) divisible by six c) divisible by twenty-one
On ten identical cards, there are numbers from zero to nine. Determine the probability that a two-digit number randomly drawn from the given cards is: a) even b) divisible by six c) divisible by twenty-one - Dice same probability
 We have a dummy die where numbers fall with probabilities P (1)=0.1; P (2)=0.2; P (3)=0.22; P (4)=0.16; P (5)=0.24; P (6)=0.08. Determine the probability that the two toss the same numbers.
We have a dummy die where numbers fall with probabilities P (1)=0.1; P (2)=0.2; P (3)=0.22; P (4)=0.16; P (5)=0.24; P (6)=0.08. Determine the probability that the two toss the same numbers. - Family children probability
 We randomly choose a family with three children. We distinguish between gender and age. Determine the probability that: a) the youngest girl will be among the children b) all children will be of the same sex
We randomly choose a family with three children. We distinguish between gender and age. Determine the probability that: a) the youngest girl will be among the children b) all children will be of the same sex - Probability - on the roll
 Find the probability that one will fall at least once in three rolls.
Find the probability that one will fall at least once in three rolls. - Loan pay back
 Imagine a situation a student got access to a student loan of about 1000000 naira to pay all his fees throughout his undergraduate studies without having an extra year. He is expected to pay back the money five years after securing a job, and it took him
Imagine a situation a student got access to a student loan of about 1000000 naira to pay all his fees throughout his undergraduate studies without having an extra year. He is expected to pay back the money five years after securing a job, and it took him - Apples and bananas
 If you pay $11 for one apple and nine bananas and $7 for three apples and one banana, how much do an apple and banana cost?
If you pay $11 for one apple and nine bananas and $7 for three apples and one banana, how much do an apple and banana cost? - Cucumber box order
 The merchant ordered 62 boxes of cucumbers from a vegetable grower. He wants to take 38 more boxes than small ones. How many individual boxes of cucumbers did the merchant order?
The merchant ordered 62 boxes of cucumbers from a vegetable grower. He wants to take 38 more boxes than small ones. How many individual boxes of cucumbers did the merchant order? - Shopping trips
 Luke bought some fresh produce. He picked up two oranges and three bananas. The cost of Luke's shopping was $18. Georgia also went to the same shop and bought five oranges and seven bananas. The cost of Georgia's shopping was $44. Write and solve a system
Luke bought some fresh produce. He picked up two oranges and three bananas. The cost of Luke's shopping was $18. Georgia also went to the same shop and bought five oranges and seven bananas. The cost of Georgia's shopping was $44. Write and solve a system - RT = legs, circle
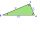 One leg of a right triangle ABC has length a= 14 cm and the radius of the circle inscribed in this triangle r= 5 cm. Calculate the length of the hypotenuse and its other leg.
One leg of a right triangle ABC has length a= 14 cm and the radius of the circle inscribed in this triangle r= 5 cm. Calculate the length of the hypotenuse and its other leg. - Rectangle circle ratio
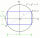 The lengths of the sides AB and AD of the rectangle ABCD are in the ratio 3:4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle.
The lengths of the sides AB and AD of the rectangle ABCD are in the ratio 3:4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle. - Fertilizer mixture
 A fruit company uses two types of fertilizers in an orange grove, brand A and brand B. each bag of brand A contains 8 pounds of nitrogen and 4 pounds of phosphoric acid. Each bag of brand B contains 7 pounds of nitrogen and 6 pounds of phosphoric acid. Th
A fruit company uses two types of fertilizers in an orange grove, brand A and brand B. each bag of brand A contains 8 pounds of nitrogen and 4 pounds of phosphoric acid. Each bag of brand B contains 7 pounds of nitrogen and 6 pounds of phosphoric acid. Th - Variation element increase
 If we increase the number of elements by 2, the number of variations of the second class without repetition increases by 22. How many elements do we have initially?
If we increase the number of elements by 2, the number of variations of the second class without repetition increases by 22. How many elements do we have initially? - Combinations - elements
 If we increase the number of elements by 1, the number of combinations of the third class without repetitions increases by 10. How many elements do we have?
If we increase the number of elements by 1, the number of combinations of the third class without repetitions increases by 10. How many elements do we have? - An account
 Seth has $9,399 in an account. The interest rate is 4 17/20% compounded annually. To the nearest cent, how much will he have in 2 years?
Seth has $9,399 in an account. The interest rate is 4 17/20% compounded annually. To the nearest cent, how much will he have in 2 years?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
