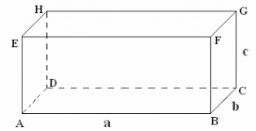
Quadrilateral 4S prism
The edge lengths of a quadrilateral prism are in the ratio a:b:c = 2:4:5. The surface of the prism is 57 cm2. Calculate the volume.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Quadrangular prism
The regular quadrangular prism has a base edge of 7.1 cm and a side edge of 18.2 cm long. Calculate its volume and surface area. - Quadrilateral prism
Calculate the volume and surface area of a regular quadrilateral prism with base edge a=24 cm if the body diagonal makes an angle of 66° with the base. - Trapezoidal base
Calculate the surface and volume of a quadrilateral prism with a trapezoidal base, where a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, the height of trapezium v = 3.7 cm, and the height of the prism h = 5 cm. - Quadrilateral 25201
Calculate the volume and surface of a regular quadrilateral prism with a base edge a = 46 mm and a height v = 0.67 dm. - Cuboid edges
Calculate the volume and surface of a cuboid whose edge lengths are in the ratio 2:3:4 and the longest edge measures 10cm. - Quadrilateral 24541
There are 50 liters of water in a filled container in the shape of a regular quadrilateral prism. Determine the height of the water if the edge of the base a = 25 cm. - Tetrahedral prism
Calculate the surface and volume of a tetrahedral prism, which has a rhomboid-shaped base, and its dimensions are a = 12 cm, b = 7 cm, ha = 6 cm, and prism height h = 10 cm.
