Intersection of sets - practice problems - page 6 of 10

Number of problems found: 195

Subtracting sets
For two sets K, L is true: K has 30 elements, L has 27 elements, and the set L - K has 22 elements. How many elements does the set K - L have?
Following 34291
The following holds for two non-empty sets, A and B: A ∪ B has 16 elements, A ∩ B has 11 elements, and the set A - B is empty. How many elements does set B-A to have?
Venn diagram
University students choose a foreign language for the 1st year. Of the 120 enrolled students, 75 chose English, 65 German, and 40 both English and German. Using the Venn diagram, determine: - how many of the enrolled students chose English only - how many
Language courses
Of the company's 60 employees, 28 attend an English course, 17 take a German course, and 20 do not attend any of these courses. How many employees attend both courses?
Perpendicular projection
Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0.
Inequality: 33371
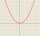Solve the quadratic inequality: -2x² + 4x + 6
Construction 32971
There is any circle k that does not have a marked center. Use a suitable construction to find the center of the circle k. Try on two different circles.
Convex lens
The convex lens consists of two spherical segments (dimensions given in mm). Calculate its weight if the density of the glass is 2.5 g/cm³. Dimensions: 60mm in length and width of the upper part 5mm, the width of the lower part 8mm
The intersection of the diagonals
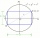In the rectangular coordinate system, a rectangle ABCD is drawn. These coordinates determine the vertices of the rectangle: A = (2.2) B = (8.2) C = (8.6) D = (2.6) Find the coordinates of the intersection of the diagonals of the ABCD rectangle.
Diagonal of the diamond
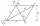The ABCD diamond shape is known as diagonal u2 and a height v. Do an analysis.
Sphere in cone
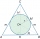A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
Line intersect segment
Decide whether the line p : x + 2 y - 7 = 0 intersects the line segment given by points A[1, 1] and B[5, 3]
Hazard game
In the Sportka hazard game, six numbers out of 49 are drawn. What is the probability that we will win: a) second prize (we guess five numbers correctly) b) the third prize (we guess four numbers correctly)?
Construction of trapezoid
Construct a trapezoid if b = 4cm, c = 7cm, d = 4,5cm, v = 3 cm (Procedure, discussion, sketch, analysis, construction)
The box
The box contains five chocolate, three fruit, and two menthol candies. We choose sweets at random from the box. What probability will we take out one chocolate, one fruit, and one menthol candy without a return?
Intersections 3
Find the intersections of the circles x² + y² + 6 x - 10 y + 9 = 0 and x² + y² + 18 x + 4 y + 21 = 0
Square and circles
The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a.
Intersections 26781
A rectangular grid consists of two mutually perpendicular systems of parallel lines with a distance of 2. We throw a circle with a diameter of 1 on this plane. Calculate the probability that this circle: a) overlaps one of the straight lines; b) do any of
Coordinates
Determine the coordinates of the vertices and the area of the parallelogram, the two sides of which lie on the lines 8x + 3y + 1 = 0, 2x + y-1 = 0, and the diagonal on the line 3x + 2y + 3 = 0
Probability
In a batch of 500 products, there are 10 rejects. In a statistical inspection, 40 products are checked, which are randomly selected from a batch, and the selection is made without repetition. The batch is considered satisfactory if there is at most one de

Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.