Math practice for 13 year olds - page 218 of 422
Number of problems found: 8427
- Container with water
 The cube-shaped container is filled with water to half its height. If we add 20 liters of water, the company will fill the container to three-quarters of its height. What is the volume of the whole container?
The cube-shaped container is filled with water to half its height. If we add 20 liters of water, the company will fill the container to three-quarters of its height. What is the volume of the whole container? - Components 15751
 Two workers produce 138 parts in one shift. At the same time, the first of them produces 30% more than the second. How many components will each have? I need a notation and an equation.
Two workers produce 138 parts in one shift. At the same time, the first of them produces 30% more than the second. How many components will each have? I need a notation and an equation. - Pedestrian 15741
 Cities A and B are 42 km apart. A pedestrian exits city A at a speed of 6 km/h in the opposite direction to city B. 30 minutes later, and a cyclist exits B following the pedestrian at a speed of 24 km/h. How many hours does the cyclist reach the pedestria
Cities A and B are 42 km apart. A pedestrian exits city A at a speed of 6 km/h in the opposite direction to city B. 30 minutes later, and a cyclist exits B following the pedestrian at a speed of 24 km/h. How many hours does the cyclist reach the pedestria - Children 15723
 There were children in the camp. 2/3 of the children went on a trip, 1/7 went swimming, and X went to the gym. How many children were in the camp?
There were children in the camp. 2/3 of the children went on a trip, 1/7 went swimming, and X went to the gym. How many children were in the camp? - Diameters 15683
 How many ball shots with diameters of 2 mm can be made of 1 kg of special metal alloy with a density of r = 7550 kg/m³?
How many ball shots with diameters of 2 mm can be made of 1 kg of special metal alloy with a density of r = 7550 kg/m³? - Consumption 15663
 The cone-shaped sheet metal roof has a base diameter of 80 cm and a height of 60 cm. If 1 kg of paint is consumed per 6 m² of sheet metal, calculate the paint consumption for painting this roof.
The cone-shaped sheet metal roof has a base diameter of 80 cm and a height of 60 cm. If 1 kg of paint is consumed per 6 m² of sheet metal, calculate the paint consumption for painting this roof. - Pyramid-shaped 15643
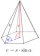 The regular quadrilateral pyramid-shaped casting, with a base edge 60 cm in length and 5 cm in height, is made of a material density of 7.8 g / cm 3. Calculate its weight.
The regular quadrilateral pyramid-shaped casting, with a base edge 60 cm in length and 5 cm in height, is made of a material density of 7.8 g / cm 3. Calculate its weight. - Father and daughter
 The father is 36 years old; the daughter is 20 years younger. What will be the ratio between them if they are ten years older?
The father is 36 years old; the daughter is 20 years younger. What will be the ratio between them if they are ten years older? - Average speed
 The average speed of a pedestrian who walked 10 km was 5km/h, and the average speed of a cyclist on the same track was 20km/h. In how many minutes did the route take more than a cyclist? Q
The average speed of a pedestrian who walked 10 km was 5km/h, and the average speed of a cyclist on the same track was 20km/h. In how many minutes did the route take more than a cyclist? Q - Hexagonal pyramid
 Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm.
Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. - Nitrogen
 One bag of urea containing 46 percent nitrogen weighs 25 kg. How many bags must be purchased for fertilizing a field of 41003 square meters if the nitrogen dose is 50.0 kg per hectare?
One bag of urea containing 46 percent nitrogen weighs 25 kg. How many bags must be purchased for fertilizing a field of 41003 square meters if the nitrogen dose is 50.0 kg per hectare? - Two chords
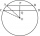 Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords.
Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - 3/8 off
 The shirt costs 38.95. If it has a discount tag for 3/8 off, how much will you pay? Round to the nearest cent.
The shirt costs 38.95. If it has a discount tag for 3/8 off, how much will you pay? Round to the nearest cent. - Rectangular base pyramid
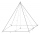 The pyramid has a rectangular base of 2.8 m and 1.4 m and a height of 2.5 meters. Calculate an area of the shell of the pyramid.
The pyramid has a rectangular base of 2.8 m and 1.4 m and a height of 2.5 meters. Calculate an area of the shell of the pyramid. - Hexa pyramid
 The base of the regular pyramid is a hexagon, which can be described as a circle with a radius of 2 m. Find the volume of the pyramid to be 2.5 m high.
The base of the regular pyramid is a hexagon, which can be described as a circle with a radius of 2 m. Find the volume of the pyramid to be 2.5 m high. - Triangular prism
 Calculate the surface of a triangular prism with the base of an equilateral triangle with a side length of 7.5 cm and a corresponding height of 6.5 cm. Prism height is 15cm.
Calculate the surface of a triangular prism with the base of an equilateral triangle with a side length of 7.5 cm and a corresponding height of 6.5 cm. Prism height is 15cm. - Two accounts
 Two accounts in the bank, one per year interest 2%, the second 3%. Total interest income 1900 USD. If we reversed interest rates, the yield would be USD 200 higher. What are the amounts on each account?
Two accounts in the bank, one per year interest 2%, the second 3%. Total interest income 1900 USD. If we reversed interest rates, the yield would be USD 200 higher. What are the amounts on each account? - Accommodated 15223
 A total of 17 pupils are accommodated in 5 rooms in the dormitory. Some rooms are triple, some quadruple. Determine how many pupils are accommodated in triple rooms.
A total of 17 pupils are accommodated in 5 rooms in the dormitory. Some rooms are triple, some quadruple. Determine how many pupils are accommodated in triple rooms. - Buttons
 The men's shirt has nine buttons, and the blouse has three buttons. Together they sewed 60 pieces and consumed 390 buttons. How many shirts?
The men's shirt has nine buttons, and the blouse has three buttons. Together they sewed 60 pieces and consumed 390 buttons. How many shirts? - Distance 15203
 In the plane, the points A, B, and C are given 3 cm apart, and they do not lie in the same straight line. Mark the set of all points whose distance from all three points is less than or equal to 2.5 cm.
In the plane, the points A, B, and C are given 3 cm apart, and they do not lie in the same straight line. Mark the set of all points whose distance from all three points is less than or equal to 2.5 cm.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
