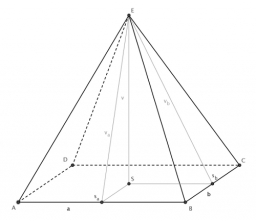
Rectangular base pyramid
The pyramid has a rectangular base of 2.8 m and 1.4 m and a height of 2.5 meters. Calculate an area of the shell of the pyramid.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- The quadrilateral pyramid
The quadrilateral pyramid has a rectangular base of 24 cm x 3.2dm and a body height of 0.4m. Calculate its volume and surface area. - Quadrilateral pyramid,
A quadrilateral pyramid has a rectangular base with 24 cm and 13 cm dimensions. The height of the pyramid is 18cm. Calculate 1/the area of the base 2/casing area 3/pyramid surface 4/volume of the pyramid - Quadrilateral 19413
Calculate the surface area of a regular quadrilateral pyramid given: a= 3.2 cm h= 19 cm Method: 1) calculation of the height of the side wall 2) area of the base 3) shell areas 4) the surface of a regular quadrilateral pyramid - Consumption 17823
The roof is a regular hexagonal pyramid shell with a wall height of v = 5 m and a base edge of a = 4 m. Calculate the consumption of sheet metal to cover the roof, assuming 15% losses.
- Rectangular base - II
Calculate the volume of a pyramid with a rectangular base with sides a = 7 cm, b = 5 cm, and height of the pyramid v = 13 cm. - Quadrilateral pyramid
Calculate the volume of a regular quadrilateral pyramid, which has the size of the base edge a = 12 cm and a height of 11 cm. - Quadrilateral pyramid
Calculate the surface of a quadrilateral pyramid with a rectangular base, dimensions a = 8 cm, b = 6 cm, and height H = 10 cm.
