Consumption 17823
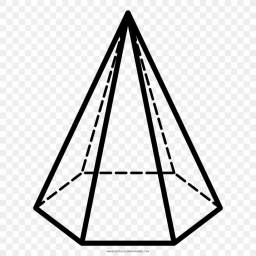
The roof is a regular hexagonal pyramid shell with a wall height of v = 5 m and a base edge of a = 4 m. Calculate the consumption of sheet metal to cover the roof, assuming 15% losses.
Correct answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Consumption 69174
The tower's roof has the shape of the shell of a rotating cone with a base diameter of 4.3 m. The deviation of the side from the plane of the base is 36°. Calculate the consumption of sheet metal to cover the roof, assuming 8% for waste. - Tower
The top of the tower is a regular hexagonal pyramid with a base edge 6.1 meters long and a height 11.7 meters. How many m² of the sheet is required to cover the top of the tower? We must add 9% of metal for waste. - Four-sided 7910
The roof of the recreation cottage has the shape of a regular four-sided pyramid with a height of 8m and a base edge of 4m. How much ℅ went to folds and joints, and 75.9 square meters of sheet metal were used to cover the roof? - Top of the tower
The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join
- Regular hexagonal pyramid
Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height of w = 20cm. Sketch a picture. - Wall height
Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height w = 20 cm. - Four-sided 5957
How much m² of the galvanized sheet is used to cover the roof of the tower, which has the shape of a four-sided pyramid, whose base edge is 6 m long? The height of the tower is 9m. When covering, is 5% metal waste expected?
