Tower
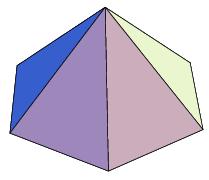
The top of the tower is a regular hexagonal pyramid with a base edge 5.7 meters long and a height 7 meters. How many m2 of the sheet is required to cover the top of the tower? We must add 4% of metal for waste.
Final Answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Top of the tower
The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join - Four-sided turret The turret has the shape of a regular four-sided pyramid with a base edge 0.8 m long. The height of the turret is 1.2 m. How many square meters are needed to cover it, counting the extra 10% sheet metal waste?
- Consumption 17823
The roof is a regular hexagonal pyramid shell with a wall height of v = 5 m and a base edge of a = 4 m. Calculate the consumption of sheet metal to cover the roof, assuming 15% losses. - Four-sided 7833
The tower has the shape of a regular four-sided pyramid with a base edge of 0.8 m. The height of the tower is 1.2 meters. How many square meters of sheet metal is needed for coverage if we count eight percent for joints and overlap? - Four-sided 5957
How much m² of the galvanized sheet is used to cover the roof of the tower, which has the shape of a four-sided pyramid, whose base edge is 6 m long? The height of the tower is 9m. When covering, is 5% metal waste expected? - Roof cover
Above the pavilion with a square ground plan with a side length of a = 12 m is a pyramid-shaped roof with a height v = 4.5 m. Calculate how much m² of sheet metal is needed to cover this roof; if 5.5% of the sheet, we must add for joints and waste. - Church roof
The roof of the church tower has the shape of a regular tetrahedral pyramid with a base edge length of 5.4 meters and a height of 5 m. It was found that the 27% covering of the roof area needs to be corrected. What amount of material will be required?
