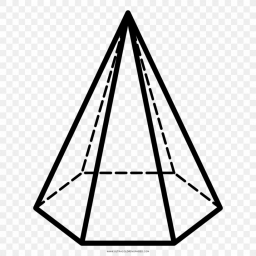
Regular hexagonal pyramid
Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height of w = 20cm. Sketch a picture.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Hexagonal pyramid
Please calculate the height of a regular hexagonal pyramid with a base edge of 5cm and a wall height of w = 20cm. Please sketch a picture. - Quadrilateral pyramid
Find the height and surface of a regular quadrilateral pyramid with a base edge a = 8cm and a wall height w = 10cm. Sketch a picture. - Hexagonal 13891
A regular hexagonal pyramid has a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. Please sketch the picture. Please calculate the surface of a regular hexagonal pyramid. - Wall height Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height w = 20 cm.
- Consumption 17823
The roof is a regular hexagonal pyramid shell with a wall height of v = 5 m and a base edge of a = 4 m. Calculate the consumption of sheet metal to cover the roof, assuming 15% losses. - Hexagonal pyramid
Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm. - Quadrilateral 8221
Calculate the height and surface of a regular quadrilateral pyramid with a base edge a = 8 cm and a wall height w = 10 cm.
