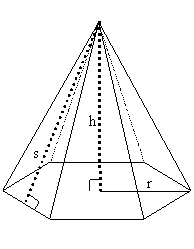
Hexagonal pyramid

Please calculate the height of a regular hexagonal pyramid with a base edge of 5cm and a wall height of w = 20cm. Please sketch a picture.

Correct answer:

h =  19.5256 cm

Step-by-step explanation:

$$\begin{gathered} a=5\text{ cm } \\ w=20\text{ cm } \\ r=a=5\text{ cm } \\ {s}^2=(a\mathrm{/}2{)}^2+w^2 \\ s=\sqrt{(a\mathrm{/}2{)}^2+w^2}=\sqrt{(5\mathrm{/}2{)}^2+20^2}\doteq 20.1556\text{ cm } \\ {s}^2=r^2+h^2 \\ h=\sqrt{s^2-r^2}=\sqrt{20.1556^2-5^2}=19.5256\text{ cm} \end{gathered}$$

Try another example

Related math problems and questions:

• Regular hexagonal pyramid
  Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height of w = 20cm. Sketch a picture.
• Wall height
  Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height w = 20 cm.
• Hexagonal pyramid
  Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm.
• Hexagonal pyramid
  Find the volume of a regular hexagonal pyramid, the base edge of which is 12 cm long and the side edge 20 cm.
• Hexagonal pyramid
  Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm.
• Quadrilateral pyramid
  Find the height and surface of a regular quadrilateral pyramid with a base edge a = 8cm and a wall height w = 10cm. Sketch a picture.
• Pentagonal pyramid
  The height of a regular pentagonal pyramid is as long as the edge of the base, 20 cm. Calculate the volume and surface area of the pyramid.
• Hexagonal pyramid
  Find the area of a shell of the regular hexagonal pyramid, if you know that its base edge is 5 cm long and the height of this pyramid is 10 cm.
• Pyramid 8
  Calculate the volume and the surface area of a regular quadrangular pyramid with the base side 9 cm and side wall with the base has an angle 75°.
• Hexagon cut pyramid
  Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm.
• Pyramid height
  Find the volume of a regular triangular pyramid with edge length a = 12cm and pyramid height h = 20cm.
• Tetrahedral pyramid
  It is given a regular tetrahedral pyramid with a base edge of 6 cm and the height of the pyramid 10 cm. Calculate the length of its side edges.
• 9-gon pyramid
  Calculate the volume and the surface of a nine-sided pyramid, the base of which can be inscribed with a circle with radius ρ = 7.2 cm and whose side edge s = 10.9 cm.
• Regular quadrilateral pyramid
  What is the volume of a regular quadrilateral pyramid if the edge of the base is 8 cm long and the height of the side wall is 5 cm?
• Hexagonal pyramid
  Regular hexagonal pyramid has dimensions: length edge of the base a = 1.8 dm and the height of the pyramid = 2.4 dm. Calculate the surface area and volume of a pyramid.
• Hexagonal pyramid
  Calculate the volume and surface area of a regular hexagonal pyramid with a base edge a = 30 m and a side edge b = 50 m.
• Triangular pyramid
  Calculate the volume of a regular triangular pyramid with edge length a = 12cm and pyramid height v = 20cm.