Math practice for 13 year olds - page 46 of 429

Number of problems found: 8565

Daniel 3
Daniel and Eva earned 180 euros together. Daniel earned 70 euros more than Eva. How much did Daniel earn, and how much did Eva earn?
Matej 2
Matej, Marko, Milan, and Matúš had a total of 205 football player cards with signatures. Marko has four times more than Matej. Matúš had two times less than Marko. Milan had 20 cards less than Matúš. How many cards did each have?
Calculate 263
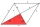Calculate the area of a rhombus whose diagonals are u=12, v=19
In the domestic
In the domestic express train, there are 1st and 2nd class carriages. There are 2x more 2nd class carriages than 1st class. There are 10 compartments in each carriage. In 1st class, each compartment has 6 seats, and in 2nd class carriages, there are eight
Average time
Determine the average time required in minutes for one product, if it is known that 6 workers need 8 minutes, 15 workers 12 minutes, 5 workers 10 minutes, and 9 workers 13 minutes.
Construct 22
Construct a rhombus ABCD if the diagonals are f=7cm, e=5 cm.
Two Sections
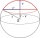A sphere with a radius of 5 cm was divided into two spherical sections. The height of the smaller section is 1cm. Determine the volume of the smaller section to the nearest hundredth of a cm³.
To the cinema 2
On Tuesday, 20 more visitors came to the cinema than on Monday. On Wednesday, half as many visitors came as on Tuesday. There were a total of 175 visitors to the cinema during these three days. How many were there each day?
Members 2
The members of a housing cooperative elected a seven-member board. In how many ways can a chairman, vice-chairman, treasurer, and recorder be chosen from among them?
Books in Slovak and English
Vlasta has 4 Czech and 3 English books. She wants to arrange them on a shelf so that Slovak books are first and then English books are second. How many ways are there to do this?
Birthday boy 2
In how many ways can seven people be seated around a table so that the birthday boy sits at the head?
HAMMER 3
Determine how many ways it is possible to rearrange the letters of the word HAMMER so that in this rearrangement some group of consecutive letters forms the word WATER.
Base RR odd
The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm.
Relay
The relay race will be run for the class of Katka, Alice, Michaela, and Erika. Determine how many different orders there are in which the girls can run, as long as each of them can run in any position.
Police on time
A boat with smugglers has left the shore and is traveling at a speed of 85 km/h. In 10 minutes, a police boat starts chasing it at a speed of 110 km/h. International waters, where the possibility of apprehending smugglers ends, begin 30 km from the coast.
Map - route
The map has a scale of 1:40000. In how many centimeters will the route, which measures 4.8 km, be shown on it?
Tanker 3
A gasoline tank weighs 4500kg. If we pump 30% of the gasoline out of the tank, it will weigh 3900kg. How many kilograms does an empty tank weigh?
RR trapezoid 12
In an isosceles trapezoid ABCD, calculate the missing lengths of the sides when a=46cm, b=85cm height=84cm.
Beads
We have 4 beads. One is green, one is yellow, and 2 are pink. In how many possible ways can we string them on a string?
Segments 6
Compare the ratio of 1cm and 1m.

Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.