Maths practice for 14 year olds - page 146 of 376
Number of problems found: 7502
- Surface area and volume
Find the surface area and volume of a rotating cone whose diameter is 60 mm and side length is 3.4 cm. - Product selection ways
Among the 24 products, seven are defective. How many ways can we choose to check a) 7 products so that they are all good b) 7 products so that they are all defective c) 3 good and two defective products? - A license
A license plate has
three letters followed by four numbers. Repeats are not allowed for the letters, but they are for the numbers. If they are issued at random, what is the probability that the three letters are in alphabetical order and the three number - School parliament
There are 18 boys and 14 girls in the class. In how many ways can three representatives be elected to the school parliament if these are to be: a) the boys themselves b) one boy and two girls - Total area
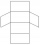Calculate the total area (surface and bases) of a prism whose base is a rhombus with 12cm and 18cm diagonals and whose prism height is 10 cm. - Sequentially pick
There are 6 different tickets marked with numbers 1 to 6 in the pocket. In how many different ways can we sequentially, taking into account the order, choose three of them, if the chosen tickets return to the pocket? - The land
The owner wants to divide the land with dimensions of 220 m and 308 m into equally large square plots with the largest possible area. How long will one side of the plot be? - Iglu - cone tent
The cone-shaped tent is 3 m high, and the diameter of its base is 3.2 m. a) The tent is made of two layers of material. How many m² of fabric is needed for production (including flooring) if 20% needs to be added to the minimum amount due to cutting waste - Constant Angular Acceleration
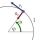The particle began to move from rest along a circle with a constant angular acceleration. After five cycles (n = 5), its angular velocity reached the value ω = 12 rad/s. Calculate the magnitude of the angular acceleration ε of this motion and the time int - Two prizes
Teacher Mae is giving away a random prize to a class of 15 pupils (7 boys and eight girls). What is the probability that girls will win both prizes? - Book reading order
Dana received four new books. How many different orders can she read them? - Round table
Eight people are sitting at a round table. In how many ways can they be seated around the table? - Medal award ways
Sixteen teams will compete in the hockey tournament. How many ways can a gold, silver, and bronze medal be awarded? - Committee selection ways
There are 24 students in the class. How many ways can we select a class committee? Where are the chairman, treasurer, and bulletin board? - Isosceles triangle
The given is an isosceles triangle with a base of 24dm and an arm of 15dm. Calculate the height of the triangle. - Ladder and wall
The ladder is 13 m long, and its lower part is 5 m away from the wall. How high does the ladder reach? - Bike distance
Places A and B are 30 km apart. From A, Peter will ride a bike at a speed of 18km/h. Milan is also a bike from B but at 24km/h speed. How far apart will they be after 20 minutes? - Hydraulic jack force
The hydraulic jack has pistons with a capacity of 6 cm² and 360 cm². How much force do we have to apply to the smaller piston to be able to lift a body weighing 180 kg on the larger piston? - Hydraulic press force The hydraulic press has pistons with a capacity of 20 cm² and 800 cm². How much force acts on the larger piston if we work on the smaller piston with a force of 100 N?
- Five-digit number creation
How many five-digit numbers do we create from digits 1, 2, and 3?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
