Reason - math word problems - page 35 of 108
Number of problems found: 2157
- Identical line
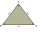 In which triangles is the line identical with the height?
In which triangles is the line identical with the height? - Sweets, candy
 Grandfather gave out sweets to four children. At the last moment, two more children came, so to have them all the same, each of the four children would receive four candies less than they would have received if they had not. How much did my grandfather ha
Grandfather gave out sweets to four children. At the last moment, two more children came, so to have them all the same, each of the four children would receive four candies less than they would have received if they had not. How much did my grandfather ha - The orchard
 Four temporary workers harvested the orchard in 9 days. How many temporary workers do we need for six days?
Four temporary workers harvested the orchard in 9 days. How many temporary workers do we need for six days? - Timetable 20313
 The train ran the distance between stations at a 90km/h speed in 4 hours. What speed can it take if the journey takes an hour longer according to the new timetable?
The train ran the distance between stations at a 90km/h speed in 4 hours. What speed can it take if the journey takes an hour longer according to the new timetable? - Troops
 The tourist group has two leaders, with an average age of 30, and several children, with an average age of 10. The total age of the group is 12. How many children are in the group?
The tourist group has two leaders, with an average age of 30, and several children, with an average age of 10. The total age of the group is 12. How many children are in the group? - Arithmetic 20153
 The teacher has 12 examples from geometry and 15 examples from arithmetic. How many papers can he create if he wants three examples from geometry and five from arithmetic in the letter?
The teacher has 12 examples from geometry and 15 examples from arithmetic. How many papers can he create if he wants three examples from geometry and five from arithmetic in the letter? - Bent scale
 Monica weighed 52 kg. Sara 54 kg. Together they weighed 111 kg. They noticed that the needle on the scale was bent. How much did they really weigh?
Monica weighed 52 kg. Sara 54 kg. Together they weighed 111 kg. They noticed that the needle on the scale was bent. How much did they really weigh? - The florist
 A consignment of 200 roses arrived at the florist in the morning. She sold more than half of them during the day. She wants to tie bouquets of the remaining roses. One rose will always be left if she ties a bouquet of three, four, five, or six roses. Dete
A consignment of 200 roses arrived at the florist in the morning. She sold more than half of them during the day. She wants to tie bouquets of the remaining roses. One rose will always be left if she ties a bouquet of three, four, five, or six roses. Dete - Apples 20043
 From 10 kg of fresh apples, we get 1.25 kg of dried. How many kg of fresh do we need per 10 kg of dried?
From 10 kg of fresh apples, we get 1.25 kg of dried. How many kg of fresh do we need per 10 kg of dried? - Four-member 20013
 Determine how many ways it is possible to form a four-member team from 6 men and four women, where there are exactly two men.
Determine how many ways it is possible to form a four-member team from 6 men and four women, where there are exactly two men. - Significant 19983
 We roll two dice, red and green. What probability will a more significant number fall on the red dice than on the green?
We roll two dice, red and green. What probability will a more significant number fall on the red dice than on the green? - Non-conforming 19863
 The probability that a quality product will meet all technical requirements is 0.95. What is the probability that all three randomly produced products will be: a) conforming, b) non-conforming
The probability that a quality product will meet all technical requirements is 0.95. What is the probability that all three randomly produced products will be: a) conforming, b) non-conforming - Marks at school
 There are 30 students in the class. Five students in the class had a mark of three or triple at the end of the math certificate, and the other students had a mark of one or two. The average mark in all students' mathematics in the class at the end of the
There are 30 students in the class. Five students in the class had a mark of three or triple at the end of the math certificate, and the other students had a mark of one or two. The average mark in all students' mathematics in the class at the end of the - Sum of the seventeen numbers
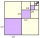 The sum of the 17 different natural numbers is 154. Determine the sum of the two largest ones.
The sum of the 17 different natural numbers is 154. Determine the sum of the two largest ones. - Equation 19683
 Fill in the signs so that equation 3 2 3 4 = 3 applies.
Fill in the signs so that equation 3 2 3 4 = 3 applies. - Integer cube
 The length of the cube edge is an integer. Its volume is in cm3, a five-digit number divisible by 1331. What is the length of the edge of this cube?
The length of the cube edge is an integer. Its volume is in cm3, a five-digit number divisible by 1331. What is the length of the edge of this cube? - Inspectors 19633
 Five inspectors will catch an average of 70 black passengers in 6 days. How many black passengers are caught by nine inspectors in 10 days?
Five inspectors will catch an average of 70 black passengers in 6 days. How many black passengers are caught by nine inspectors in 10 days? - Magnitudes 19623
 Calculate the magnitudes of the interior angles of a triangle if you know that these are in a 2:3:5 ratio.
Calculate the magnitudes of the interior angles of a triangle if you know that these are in a 2:3:5 ratio. - Calculate 19543
 Calculate the surface of a prism with a square base whose mantle is a rectangle with sides of 18cm and 8cm. How many solutions does the task have? List all solutions.
Calculate the surface of a prism with a square base whose mantle is a rectangle with sides of 18cm and 8cm. How many solutions does the task have? List all solutions. - School year
 At the beginning of the school year, 396 notebooks and 252 textbooks were ready to be distributed in the classroom. All pupils receive the same number of notebooks and the same amount of textbooks. How many pupils are there in the class if you know that t
At the beginning of the school year, 396 notebooks and 252 textbooks were ready to be distributed in the classroom. All pupils receive the same number of notebooks and the same amount of textbooks. How many pupils are there in the class if you know that t
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
