Square (second power, quadratic) - math word problems - page 29 of 150
Number of problems found: 2982
- Isosceles triangle
 Find the area of an isosceles triangle whose leg is twice the base, b=1
Find the area of an isosceles triangle whose leg is twice the base, b=1 - Evaluate 26
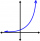 Evaluate square root: √1³+2³+3³+4³=
Evaluate square root: √1³+2³+3³+4³= - A farmer 6
 A farmer made a square chicken coop of 6 1/3m. Determine the perimeter of the chicken coop. (Recall: perimeter =add all sides)
A farmer made a square chicken coop of 6 1/3m. Determine the perimeter of the chicken coop. (Recall: perimeter =add all sides) - Square field
 The perimeter of a square field is 64 m. Find the cost of cementing the field at the cost of 240 USD per square meter.
The perimeter of a square field is 64 m. Find the cost of cementing the field at the cost of 240 USD per square meter. - Rohan
 Rohan wants to fence his square field, with 75 m on each side. Suppose the cost of 1 m of wire is Rs 1.50 per meter. Find the cost of fencing the field.
Rohan wants to fence his square field, with 75 m on each side. Suppose the cost of 1 m of wire is Rs 1.50 per meter. Find the cost of fencing the field. - Gardener 75344
 A gardener lays tiles around a square flower bed. It needs 12 tiles around the 2x2 bed. How many tiles will he need around the size of the bed? a) 9x9 b) nxn? How big was the bed for which the gardener consumed c) 112 d) 4n tiles?
A gardener lays tiles around a square flower bed. It needs 12 tiles around the 2x2 bed. How many tiles will he need around the size of the bed? a) 9x9 b) nxn? How big was the bed for which the gardener consumed c) 112 d) 4n tiles? - Rectangular 75334
 In the rectangular coordinate system, find the images of points A[-3; 2] and B[4; -5] in central symmetry according to point O[0; 0]. A. A'[3; 2], B'l-4; -5] C. A'[-3; -2], B'[4; 5] B. A'[-3; -2], B'[-4; 5] D. A'[3; -2], B'[-4; 5]
In the rectangular coordinate system, find the images of points A[-3; 2] and B[4; -5] in central symmetry according to point O[0; 0]. A. A'[3; 2], B'l-4; -5] C. A'[-3; -2], B'[4; 5] B. A'[-3; -2], B'[-4; 5] D. A'[3; -2], B'[-4; 5] - A yard
 Yevgen is fencing in a yard that is 30 meters longer than it is wide. The yard will have an area of 1000 m². Find its width and length.
Yevgen is fencing in a yard that is 30 meters longer than it is wide. The yard will have an area of 1000 m². Find its width and length. - A Pile of salt
 A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile?
A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile? - The cosine law
 Solve the unknown dimensions for the following triangle: Triangle ABC: Angle A=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of
Solve the unknown dimensions for the following triangle: Triangle ABC: Angle A=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of - Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - The radius
 A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone
A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone - SAS calculation
 Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle α is 47°, find side a. Please round to one decimal.
Given the triangle ABC, if side b is 31 ft., side c is 22 ft., and angle α is 47°, find side a. Please round to one decimal. - Express value
 Given that p = √(mx/t-t² x) Make x the subject If m = 7, p = -3 and t = 4, find the value of x
Given that p = √(mx/t-t² x) Make x the subject If m = 7, p = -3 and t = 4, find the value of x - Calculate 75014
 The surface of a cube is equal to 294 square meters. Calculate the edge and volume of the cube.
The surface of a cube is equal to 294 square meters. Calculate the edge and volume of the cube. - Intersection 74914
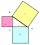 Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis.
Find the perimeter of triangle ABC, where point A begins the coordinate system. Point B is the intersection of the graph of the linear function f: y = - 3/4• x + 3 with the x-axis, and C is the intersection of the graph of this function with the y-axis. - Solve 12
 Solve the following quadratic equation: 3/2-(2x-1)²=5/4
Solve the following quadratic equation: 3/2-(2x-1)²=5/4 - Mr. Erel
 Mr. Erel earns 12% compounded quarterly. He projected to collect Ᵽ500,000 after ten years. What is the amount he needs to invest?
Mr. Erel earns 12% compounded quarterly. He projected to collect Ᵽ500,000 after ten years. What is the amount he needs to invest? - Intersection of Q2 with line
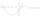 The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the
The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the - A cuboid 2
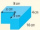 A cuboid with a depth of 4 cm but a length and width of x cm is cut out from one corner of the original cuboid as shown (the original cuboid has dimensions of 10x8x4 cm). The remaining shape has a volume of 199 cm³. Calculate the value of x.
A cuboid with a depth of 4 cm but a length and width of x cm is cut out from one corner of the original cuboid as shown (the original cuboid has dimensions of 10x8x4 cm). The remaining shape has a volume of 199 cm³. Calculate the value of x.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
